完全流体の流れ ←→ ねじれとたわみ

　弾性体と流体を合わせて連続体と呼ぶ。弾性体は，変形した物体が元の形に戻ろうとする性質（弾性）を持った物体のことで，流体は液体と気体の総称のことである。まずは弾性体についてその特徴を見ていこう。

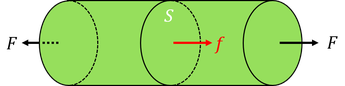
　弾性体の内部にある面積Sの断面を考える。この弾性体に力Ｆを加えたとき、この面にはたらく単位面積当たりの力ｆのことを応力と呼ぶ。応力には引っ張り応力と圧縮応力があり、引っ張り応力を正、圧縮応力を負の値で表す。また、応力の単位は圧力と同じパスカル（Pa）である。連続体の分野では、すべての方向から同じ大きさの力がはたらくとき、その応力のことを圧力と呼ぶ。

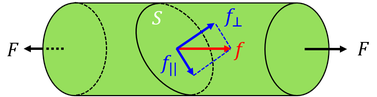
　力Fに対して斜め向きの面を考えると、応力は面に垂直な成分と平行な成分に分けることができ、垂直な成分を法線応力（垂直応力）、平行な成分を剪断応力（ずれ応力）と呼ぶ。地球物理学の分野で扱われる例としては、剪断応力が岩石の摩擦強度を超えた時に地震が起こる。

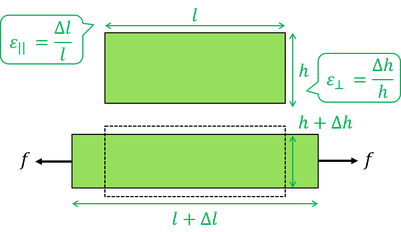
　応力を加えると物体は変形する。元の長さｌに対する変形量Δｌの比εを、ひずみという。伸びた場合が正、縮んだ場合が負である。また、ひずみεが応力ｆに比例することをフックの法則と呼び、

比例定数Eをヤング率と呼ぶ。また、応力方向のひずみと応力に垂直な方向のひずみの比σをポアソン比と呼ぶ。

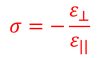
マイナスが付いているのは、縮んだ時のひずみが負の値だからである。ポアソン比は多くの物質で正の値になる。

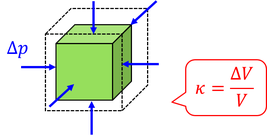
　次は体積が変化するときを考えよう。もとの体積Vに対する体積の変化量ΔVの比κを、体積ひずみという。いま、すべての方向から等しい圧力ｐが加えられているとしよう。この圧力がすべての方向で等しくΔｐだけ増加したとき、体積ひずみκは圧力変化Δｐに比例し、

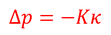
比例定数Kを体積弾性率と呼ぶ。

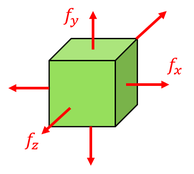
　体積V=xyzの直方体に図のような応力がはたらいているとき、x方向のひずみは、x方向の応力によるものの他に、y方向、ｚ方向の応力による影響を考える必要がある。

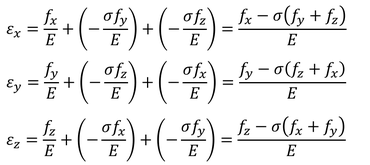
　これらを使って体積ひずみを計算してみよう。すると

となる。途中でひずみの2乗や3乗は非常に小さいので省略した。この式から、ポアソン比σ=1/2の物質の体積ひずみはκ=0となり、体積が変化しないことが分かる。また、3方向の応力がすべて－Δpであるとき、体積ひずみは

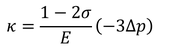
となるので、この式を

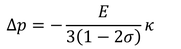
と変形することで、体積弾性率

を得る。体積弾性率K＞0のときσ＜－1/2である。

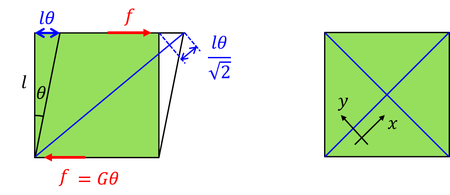
　次は、一辺ｌの立方体の上面と下面に剪断応力ｆを加えたずれ変形を考える。ずれ変形はずれ角θで表すことができ、剪断応力ｆはずれ角θに比例する。また、比例定数Ｇは剛性率と呼ばれる。剛性率が∞の物質は変形しない剛体である。ここで、ずれ変形によって伸びる方向にｘ軸、縮む方向にｙ軸を取ると、ｘ軸方向のひずみは

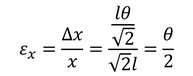
と表される。

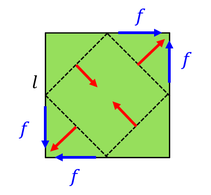
　ところで、上面と下面に剪断応力がはたらいているだけだと、この弾性体は回転してしまう。それを防ぐため、左右の面にも同じ大きさの応力がはたらいているとする。このことを踏まえて、ｘ軸方向の引っ張り応力を求めると、

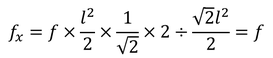
となる。同様に、ｙ軸方向の圧縮応力は－ｆである。ここで、ｚ軸方向の応力は０だから

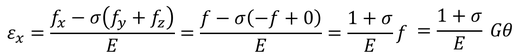
となり、θ/2と比較することで剛性率Ｇ

を得る。この式から、G＞０のときσ＞－1となるので、先に求めた範囲と合わせてポアソン比は

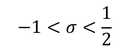
であることが分かる。σ＝－1の物質は体積が変化しても形が変わらないことを示している。