ねじれとたわみ
前回は弾性体にはたらく応力と生じたひずみの関係と,体積変化,ずれ変形について見てきた。今回は,ねじれ,曲げ,たわみについて見ていこう。
ねじれ
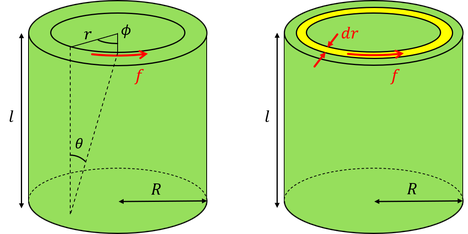
底面の半径R,高さlの円柱をねじることを考えよう。半径r,中心角φに対応するずれはrφで,高さl,ずれ角θに対応するずれはlθである。これらが等しいことから
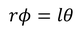
の関係がある。これを用いて応力fを表すと
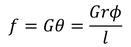
となる。Gは剛性率である。続いて,厚さdrのリング状の部分(面積2πrdr)に注目して,この部分に応力fがはたらいているとすると、その力は
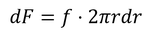
と計算でき,この力による力のモーメントは
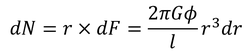
である。断面全体の力のモーメントを求めるには,r=0~Rの範囲でこれを積分すればよい。
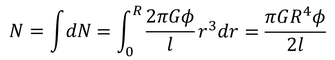
このことから,円柱の半径Rが小さいほど,ねじれ角φが大きくなることが分かる。
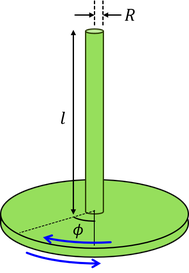
ねじった円柱から手をはなすと,円柱のねじれがもとに戻り,しばらくして逆向きにねじれるという往復運動をする。これを,ねじれ振動と呼ぶ。では,この振動の周期Tを求めてみよう。まず,回転運動の運動方程式を立て,角加速度αを求める。


マイナスが付くのは,つり合いの位置に戻ろうとする向きだからである。ここで,両辺にRを掛けると
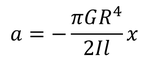
こうして円柱の外側部分の加速度aと変位xの関係が得られる。これを単振動の基本式と比較することで,角振動数
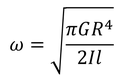
および周期
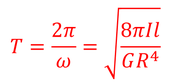
を得る。
曲げ
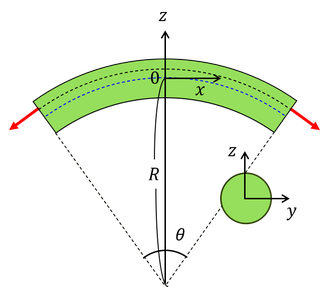
続いて,棒を曲げることを考えよう。図のように曲げるとき,外側は伸び,内側は縮むが,その間の長さが変化しない面を,中立面と呼ぶ。曲率半径R,両端の角度θであるとき,中立面から上側にzだけ離れた面のひずみは
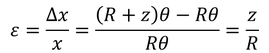
と表せる。このひずみを与える応力fは,棒のヤング率Eを用いて
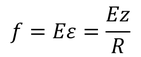
と表せ,微小な面積dydzの部分にはたらく小さな力が
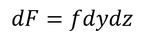
と表せるから,中立面からの小さな力のモーメントは
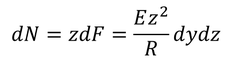
となる。この小さな力のモーメントを断面積全体で積分することで,全体の曲げモーメントが得られる。
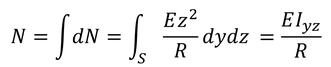
ここで,Iと置いた積分
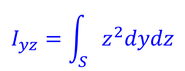
を,断面2次モーメントと呼ぶ。断面2次モーメントは力のモーメントに対する曲がりにくさを表している。
断面2次モーメント

断面2次モーメントは,断面の形によって異なる。いくつか計算してみよう。まずはa×bの長方形について考えてみる。面積dxdyの小さな部分に注目して,これを面積全体について足し合わせればいい。
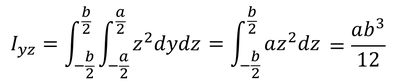
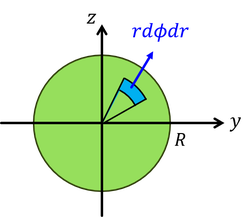
円形の断面2次モーメントを求めるには,極座標(r,φ)を用いるとよい。面積rdφdrの小さな部分に注目して,これを面積全体について足し合わせる。
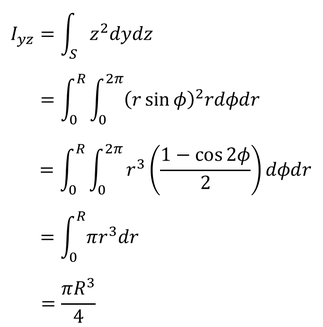
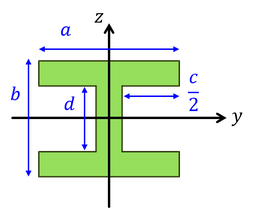
断面積に対して曲げに強いとされているのが,Hの形だ。3つの部分に分割して計算すればいい。
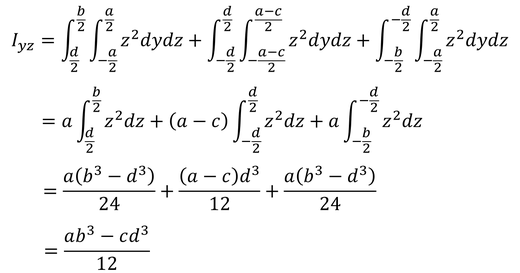
たわみ
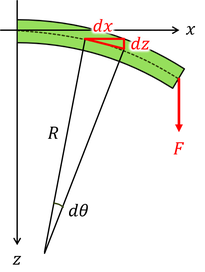
次は,一端を壁に固定した棒の他端に力Fを加えたときの棒のたわみを求めてみよう。曲率半径R,中心角dθの部分の長さは,次のように2通りの表し方ができる。
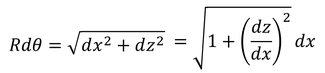
これを

の形に直しておく。また,
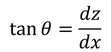
だから,これをxで微分して変形していくと
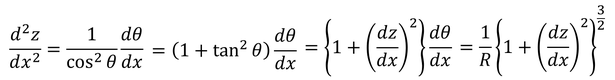
となるが,たわみは非常に小さいと考えてdz/dx≒0とすると
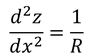
となる。ここで,
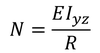
を用いると

を得る。これを,たわみ曲線の方程式と呼ぶ。
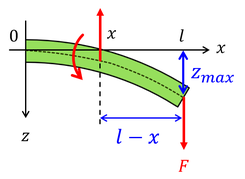
位置xに注目すると,この位置に生じる剪断応力によって,棒の断面には中立面を基準とする力のモーメントが生じる。これを曲げモーメントと呼ぶ。曲げモーメントは,位置xのまわりの力Fによる力のモーメントとつり合っている。

これをたわみ曲線の方程式へ適用して,
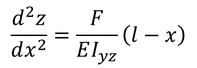
1回微分すると
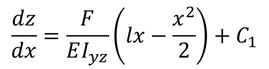
となるが,x=0付近でz方向への傾き(dz/dx)は0と考えてもよいので,積分定数はC1=0と定まる。これをもう1回積分して
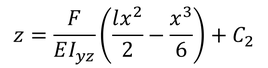
x=0のときz=0であることを用いると,積分定数C2=0が定まるので,
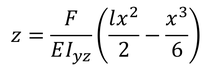
位置xにおけるたわみzが得られる。位置lにおける最大のたわみは,x=lとすればよい。
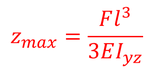
求められる。
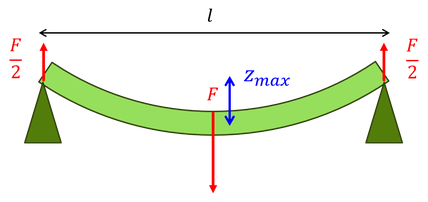
応用として,両端を支点で支えられた棒の中心に力Fを与えたときのたわみを求めてみよう。右半分に注目して上下をひっくり返すと,壁に固定された棒の問題と状況が等しくなるので,

として
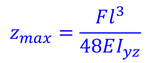
を得る。
