ストークスの抵抗法則 ←→ 応力とひずみ

　流体の速度vを、スカラー関数Φを用いて

と表せるとき、Φを速度ポテンシャルという。流速vと速度ポテンシャルΦの関係をいくつか見ていこう。

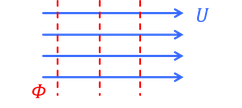
　まず、速度ポテンシャルΦが

と表されるとき、流速vは

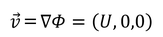
と計算できる。これはx方向の一様流である。

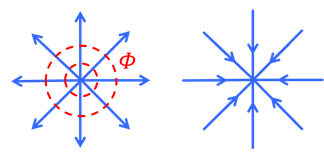
　続いて、

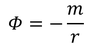
を考える。流速を極座標で表すと、

となる。m>0は湧き出し、m<0は吸い込みを表している。rは湧き出し口、吸い込み口からの距離である。また、半径Rの球体から湧き出す単位時間あたりの流量Qは、放射方向の流速を球の表面積だけ足し合わせることで、

と求められる。

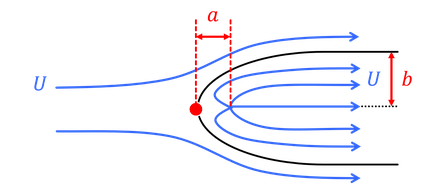
　次は、x方向の一様流と、原点からの湧き出しの和

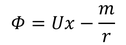
を考えよう。原点から湧き出した左向きの流速は、右向きの流速とx=－aで打ち消し合ってよどみ点を作っている。x方向の流速が、

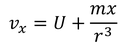
だから、x=－aのときの流速が0であることを使って、

が得られる。また、原点から湧き出した流体は半無限体から飛び出すことはない。この半無限体の断面は円で、円の半径をbとすると、湧き出す流量Qが

であることから、

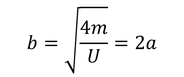
が求められる。

　湧き出しに加えて吸い込みも加えると、速度ポテンシャルは

と表される。すると、図のような閉じた領域ができる。これをランキンの卵型と呼ばれる。

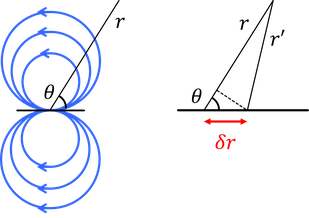
　ここで、一様流を省略すると、

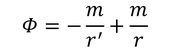
のようになるが、湧き出し口と吸い込み口がごく微小な間隔δrのときは、

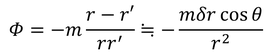
となる。ここで、

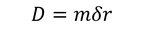
とおくと、

と表される。1点で湧き出しと吸い込みが起こっているように見えるので、これを2重湧き出しと呼ぶ。

　次は2次元の流れに限定して考えてみる。自由な経路Cに沿った速度の成分を経路Cに沿って足し合わせた量は、

と表される。経路Cが閉じているときは循環と呼ばれる。経路Cに垂直な速度の成分を足し合わせた量は、

と表され、流れの関数と呼ばれる。その理由は、経路Cを流れに沿って取ったとき、v_n=0であることから、

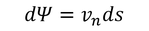
の値が0となり、ψが一定の値をとるからである。ところで、この式は

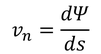
と書き換えることができる。上の図を見てわかるように、y軸正の向きにdsを取ったとき、v_nはx軸正の向きである。

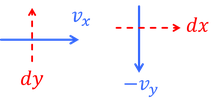
　このことを踏まえると、dx,dy,v_x,v_yの間には、

の関係があることが分かる。ところで、速度ポテンシャルΦを使うと、速度の成分が

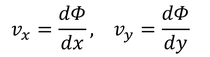
と表せたから、ψとΦの間の、

という関係が導ける。これを、コーシー・リーマンの関係式と呼ぶ。いま、複素数

について、

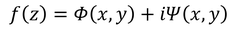
という関数を考えると、これをzによる微分が可能ということが保証される。f(z)の全微分が、

であることより、微分df/dzが、

と計算できる。ただし、

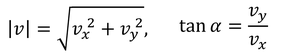
である。vを複素速度、f(z)を複素速度ポテンシャルという。

　複素速度ポテンシャルが

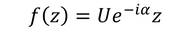
と表されるとき、df/dzは、

だから、複素速度の各成分が、

と求められる。これはx軸から角度αの向きの一様流を表している。

　次は、

を考える。ここで、

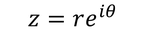
とすると、

と書けるから、

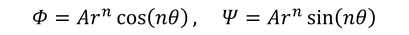
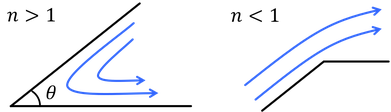
であることがわかる。流れの関数がψ=0のとき、

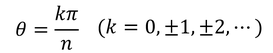
である。n>1はθ<πの角を流れる流れを表し、n<1はθ>πの角を流れる流れを表す。ところで、

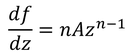
より、速度の大きさは、

である。この式から、頂点r=0での流速|v|は、n>1のとき0だが、n<1のとき∞になってしまう。実際には、凸型の角に沿って流体が流れず、剥離が起きる。

　次は、

を考える。この式から、

が得られ、半径方向、回転方向の速度が

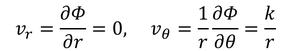
と求められる。循環を計算すると、

となる。これは渦糸と呼ばれ、反時計まわりに回転する流れを表す。

　それから、

を考えよう。これで、

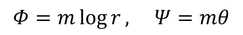
が得られるから、

半径方向と回転方向の速度が求められる。これは、湧き出しや吸い込みを表す。m>0が湧き出し、m<0が吸い込みである。半径Rの球から単位時間あたりに湧き出す流体の量を計算すると、

となる。

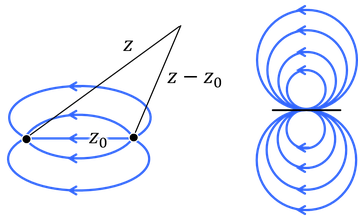
　原点に吸い込み口、そこからz_0だけ離れた場所に湧き出し口があるときを考えよう。

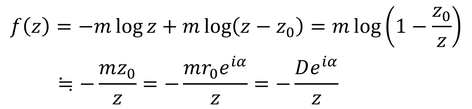
z_0が非常に小さいとして一次近似を行うとこのようになる。湧き出し口と吸い込み口がx軸上にある場合、α=0だから、

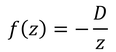
となる。

　では、一様流と二重湧き出し(上の例と湧き出し・吸い込みが逆)の和を考えよう。

これで流れの関数ψが得られ、ψ=0のとき、

原点からの距離rを求めると、

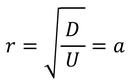
定数になる。これをaとおくと、半径aの円のまわりの流れということになる。また、

だから、これを用いると、複素速度ポテンシャルは、

になる。

　続いて、さらに循環を伴う場合を考えよう。時計回りの循環を加えると、

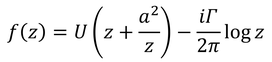
だから、複素速度が

と求められる。よどみ点(複素速度v=0)の位置を求めると、

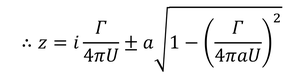
と求められる。カッコの中の正負の条件によって、よどみ点の位置と数が３種類に分類できる。

正のときは円柱の表面によどみ点は2つ、0のときは1つ、負のときは円柱から離れた位置と円柱の内部に1つずつよどみ点が存在する。また、上面のほうが速度が大きく、圧力が小さくなっている。このことから上向きの力がはたらく。これをマグナス効果と呼ぶ。

　円柱の表面での速度を求めよう。複素速度ポテンシャルが、

と表されるから、速度ポテンシャルが、

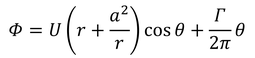
と得られ、

円柱表面での半径方向と回転方向の速度が得られる。半径方向の速度は０である。

ここで、よどみ点での圧力をp_0とすると、ベルヌーイの定理から、

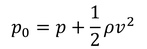
より、円柱表面での圧力pが、

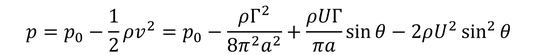
と求められる。あとは、これを演周に沿って圧力を足し合わせることで、円柱にはたらく力が得られる。流れの方向の力を抗力と呼び、

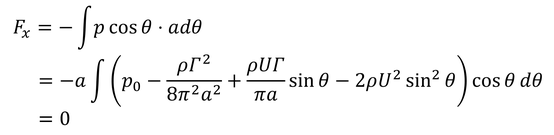
と表される。完全流体では抗力が０になる。これをダランベールのパラドックスと呼ぶ。粘性流体では０以外の値を持つ。それから、流れに垂直な方向の力を揚力と呼び、

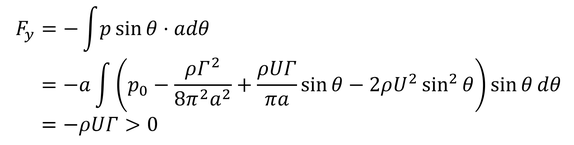
と表される。揚力がこのように表されることを、クッタ・ジューコフスキーの定理と呼ぶ。

　では、翼のような板に流体が迎角αで当たるときの揚力を求めてみよう。ジューコフスキー変換を行う。ζを用いて、

とすると、長さ4aの板をζ面に対応させると、半径aの円となる。もしx軸に平行な流れであれば、円柱のまわりの流れは、

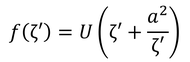
と表され、時計回りの循環を伴う場合は、

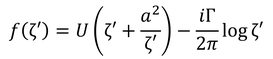
と表される。いまかんがえているのは斜めの流れだから、これを

とすればよい。これを用いれば、板のまわりの複素速度が、

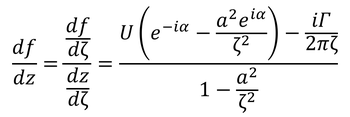
と得られる。よく見ると、ζ=±aのとき、分母が0になって複素速度が∞に発散してしまう。z面では板の両端に位置するため、板の両端で無限大の速度になるということになる。これを防ぐため、ζ=aのとき分子も0になると仮定する。

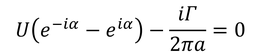
すると、このような場合の循環が

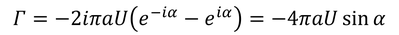
と得られ、揚力が

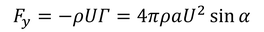
求められる。板の後端で流速が無限大にならないという条件をクッタの条件、またはジューコフスキーの仮定と呼ぶ。

迎角αが大きいほど揚力が大きいという式であるものの、現実ではαが大きくなると前端での剥離が大きくなって板の上面を流れなくなり、計算結果のような揚力がはたらかなくなってしまう。