複素数
1,2,3,…という数を自然数という。この自然数に0,-1,-2,-3,…を含めた数は整数という。今回は、実数と虚数という新たな数を導入し、それらを含めた複素数と呼ばれる数の表し方を紹介する。
解の公式
いまa≠0として、2次方程式を
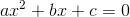
と表そう。これを平方完成して変形していけば、その答えは
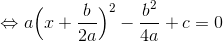
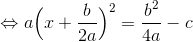
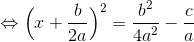
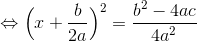
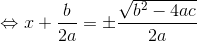

と、求めることができる。これを2次方程式の解の公式という。
ところで、この公式にはルート(√)が使われているから、このルートの中身
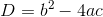
の正負によって、解の数が違ってくる。具体的には、
- D>0のとき、解は2つ
- D=0のとき、解は1つ(重解)
- D<0のとき、解はない
中学までの範囲では、ルートの中身は正でなくてはならない。だからこのように分類できるわけだ。判別に使う式ということで、このDを判別式と呼ぶ。
複素数
さっきはあえて「中学までの範囲では」と強調したが、ここからは「別にルートの中身が負になってもいいじゃないか」と考えてみよう。このような数を虚数という。虚数は、
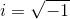
という数を使って、「2i」とか「3i」といった具合に表すことができる。このiを虚数単位という。
練習
2x2-3x+2=0の解を求めよ。
→解の公式より、

この問題の答えは、虚数単位のない部分(3/4)と、虚数単位のある部分(±√7i/4)とに分かれている。後半の虚数単位が付いている部分が虚数だから、これと比較をして前半の虚数単位が付かない数のことを実数と呼ぶことにしよう。また、実数や虚数を含めた数のまとまりを複素数という。
- 複素数Cの中に実数Rを含む(C⊃R)
- 実数Rの中に整数Zを含む (R⊃Z)
- 整数Zの中に自然数Nを含む(Z⊃N)
複素数平面
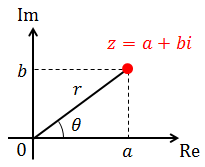
複素数zを次のように表し、
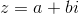
zをx-y座標に対応させたグラフ上の1点(a,b)として表したものを複素数平面という。このときのx軸を実軸、y軸を虚軸という。
また、(a,b)は(r,θ)を使って次のように表すこともできる。
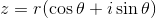
そこで次は、2種類の複素数
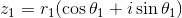

を考えて、この積を計算してみよう。
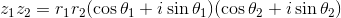
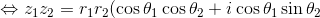
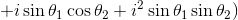
ここで、i2=-1であることに気を付けて実部と虚部に分ける。


さらに加法定理を使ってまとめれば、
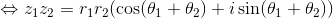
という関係が分かる。「複素数の積はθの和で表せる」という点でこの式は重要だ。
また、この式は特に、z1=z2=zのときには、
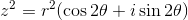
となる。
一般的に、複素数zのn乗は、

と表すことができる。これをド・モアブルの定理という。
