テイラー展開
物理では近似という作業をよく使う。例えば単振動のとき、
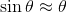
として式変形したが、これは、テイラー展開という方法を利用していたのだ。今回はその仕組みを説明してみよう。
マクローリン展開
一般的な連続関数f(x)を、
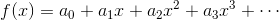
のような多項式に変形する作業をマクローリン展開という。この展開を完成させるには、それぞれの係数(a0,a1,a2,…)を求める必要がある。とりあえず、x=0とすれば、
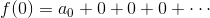
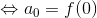
となり、a0を求めることはできる。
次にa1だが、1回微分するとxの指数が1減るということを思い出そう。つまり、f(x)の1回微分
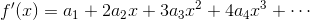
を考えるということ。こうしてしまえば、さっきと同じようにx=0とすることで、
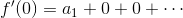

a1を求めることができる。同じように、f(x)の2回微分

についてx=0とすれば、
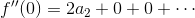

a2を求めることができ、f(x)の3回微分
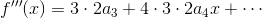
についてx=0とすれば、
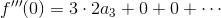

a3を求めることができる。
一般的に、f(x)のn回微分をf(n)(x)、1からnまでのすべての整数の積をn!(nの階乗)と表すことにすると、テイラー級数は、


と表すことができる。つまり、

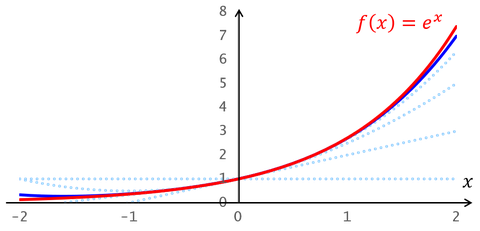
例①f(x) = ex
→まず

であり、

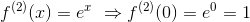
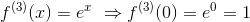
だから、
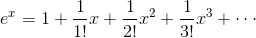
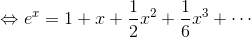

例②f(x) = sin x
→まず
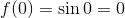
であり、
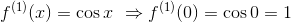
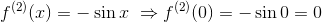

だから、
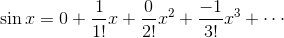


例③f(x) = cos x
→まず

であり、



だから、
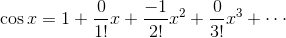
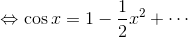
テイラー展開
いま考えた展開方法では、x=0を中心として、項が増えれば増えるほどそのフィットする範囲が広がっていく。これを「0のまわりのテイラー展開」といもいう。次は、これを任意の位置x_0のまわりのテイラー展開に修正することを考えてみよう。
とりあえず、x=x_0のときはf(x_0)になってほしいので、マクローリン展開の式

の右辺のxを、すべてx→(x-x_0)とし、定数項をf(x_0)とすればよさそうだ。また、微分f'(x)にx_0を代入していくことで次々と係数を求めるのだから、微分のf^(n)(x)の中身はx_0となる。よって、

これが、一般的な「テイラー展開」の式である。

また、この式は、f(x_0)という値に補正項を加えて、f(x)に近づけていくという操作と読み取ることもできる。ここで、x_0とxの差をΔxとすると、テイラー展開の式は次のように書き変えることもできる。
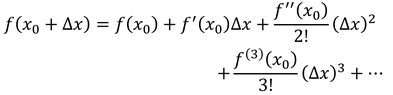
1次近似
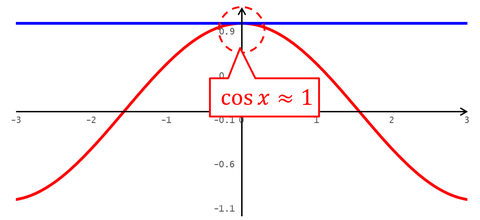

テイラー展開は、項を増やせば増やすほど、中心から離れたところまで元のグラフと合うようになっていく。ところが、項の数が増えれば増えるほど複雑になっていくので、もし中心付近の値にしか注目しないのであれば、ある程度の数で区切ってしまってもよいだろう。1次の項までを考える近似方法を、「1次近似」という。
例
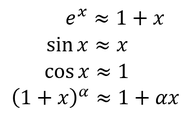
オイラーの公式
次は
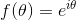
を考える。
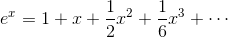
より、
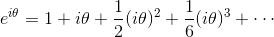
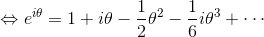
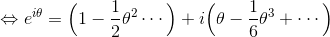
ここで、

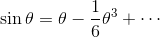
だから、
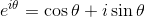
となる。これをオイラーの公式という。
特にθ=πのときには、

となる。これが有名なオイラーの等式である。
