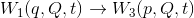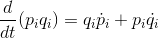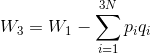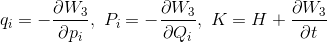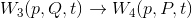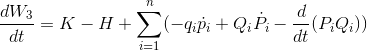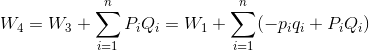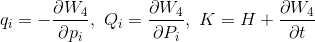正準変換
点変換
q→Qへと座標を変換する。つまり、
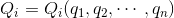
という変換を考える。このとき、ラグランジュ方程式の形は変わらない。すなわち、
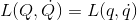
となっている。この変換を点変換という。
それでは、点変換において正準方程式の形はどう変化するのだろう。Qがqで表されるのと同様に、qもQで表せるから、
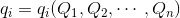
と変換することができ、


という式も成り立っている。ここで、Qに共役な運動量Pは
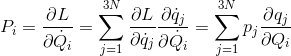
と表せるから、
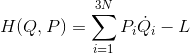



となる。これはすなわち、点変換においてハミルトンの正準方程式が形を変えないということである。
正準変換
続いて、
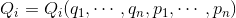

という変換を考えよう。ただし、変換後の変数(Q,P)についてもハミルトンの正準方程式が成立するような変換を考える。これを正準変換という。すなわち、新しいハミルトニアンをK(Q,P)とおいたとき、
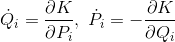
を満たす。そのためには、ラグランジアンの関係が

であればよいが、それでは制約が大きすぎるので、
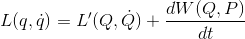
とする。ラグランジアンをハミルトニアンを使って表せば、
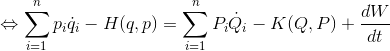
となる。これが、新旧のハミルトニアンH,Kを結び付ける関係式である。
母関数
Wは新旧の変数を結び付ける上で重要な関数である。その独立変数の取り方には、(q,Q),(q,P),(p,Q),(p,P)がある。
まず、
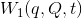
について考えて見よう。この時間微分は

だから、


よって、

という関係が成り立っている。Wは正準変換を作りだす関数と言うことで、母関数と呼ばれる。W1が陽にtを含まない場合、K=Hとなる。
続いて、母関数を

と変換しよう。上の関係式を利用してW1の時間微分dW1/dtを書きかえると、
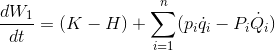
ここで、

より、
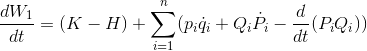
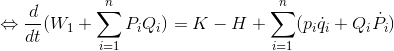
となる。さらに、
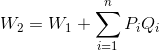
とおき、

と比較をすることで、