仮想仕事の原理
ここからは解析力学という分野を紹介しようと思う。これまで学んだ内容を微分や積分などをたっぷり使って表現し直し、扱える範囲を大幅に拡大しようというのが目的だ。さあやってみよう!
仮想仕事の原理

物体にいくつかの力がはたらき、その合力が0であるとき、物体にはたらく力はつりあっているという。

ここで、合力をFと書けば、この式は
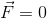
とまとめることができる。
次は、いま考えている物体を、斜面に沿って少しだけ移動させてみよう。このときの変位δrを仮想変位という。どうして仮想なのかというと、実際に動かさなくてもいいからだ。
また、合力Fと、仮想変位δrの内積

を仮想仕事という。合力F=0を維持したまま仮想変位を与えたとすれば、当然、仮想仕事もδW=0となる。

この関係が成り立つことを仮想仕事の原理という。
これの何が便利なのかというと、物体にはたらく力N,f,Wのうち、仮想変位δrに垂直な力であるNは、δrとの内積が0となるため、仮想仕事を考えることでNを無視できるのである。いまの例におけるNのような、物体の運動を制限(束縛)している力を束縛力という。
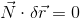

(例)
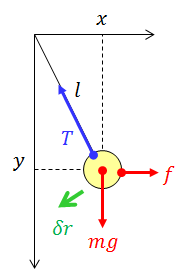
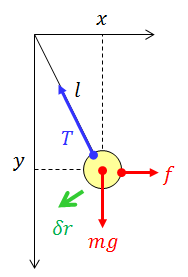
糸に取り付けられたおもりに力fを加えて、1点(x,y)で静止させた。おもりには重力mgと張力Tも働いているが、張力Tは仮想変位δrに直交するので、おもりの運動を制限する束縛力になっている。いま、仮想変位δrを

と表すと、仮想仕事の原理「δW=0」より、

という式が成り立つ。よって、力fは

となる。右辺のδy/δxは微小変位の比であり、dy/dxと計算してもよいだろう。おもりの位置は、糸の長さlを用いて
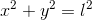
上の1点のはずだから、この式をxで微分することで、

が得られる。これをfの式へ代入して、
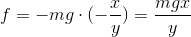
ラグランジュの未定乗数法
解析力学では、具体的な問題を一般化・抽象化し、幅広い問題に対応できるように書き換えるという作業をすることになる。
例えば、さっきの振り子の例で登場した

は、おもりの位置がこの式で表される点(x,y)上に限定されることを示している。これを束縛条件といい、束縛条件は、

のように、一般に「G=0」と表される。束縛条件は、この物体に仮想変位δrを与えたとしても、当然、成立する
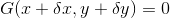
ので、束縛条件の変化dG
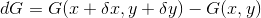
ももちろん0である(dG=0)。この変化量を全微分として表すと、
が成立していることになる。
また、束縛力以外の力Fを
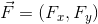
と表すと、仮想仕事の原理は、
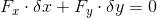
(2)
と表される。
(1)(2)式を連立方程式とみて、これを解くことを考えよう。δyの項を消去しようと思ったら、例えば(1)式を何倍かして(2)との和を計算すればいい。例えば、λ倍して足すことで、

δyの項が消せるとする。

すると、
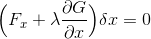
が残る。すなわち、
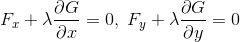
の2式を解くことで、Fなどの値が求められることが分かる。このような解法をラグランジュの未定乗数法という。
再び具体的な例に戻り、ラグランジュの未定乗数法が成り立つことを確かめよう。束縛条件

について、

だから、
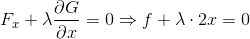

の2式を作ることができ、λを消去してfについて解けば、
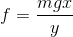
が得られ、前章の結果と等しくなっていることが分かる。難しいことは考えなくてよく、条件を公式へ代入するだけで簡単に解くことができた。このように、あらゆる問題を、機械的・解析的に解いてしまおうというのが解析力学なのだ!
ダランベールの原理
仮想仕事の原理は、物体にはたらく力がつりあっている状況で成り立つものであった。力がつりあっているとき、物体は静止か等速直線運動をする。次はさらに、これを加速度運動へ拡張しよう。
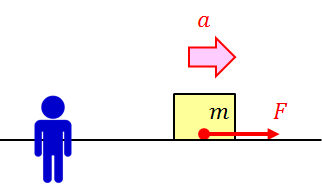
物体に力Fがはたらき、加速度aの加速度運動をしているとする。このとき、運動方程式

が成り立つことになるのだが、
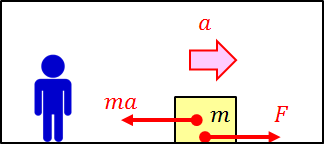
我々はすでに、加速度運動を力のつり合いの問題に置き換える方法を知っている。物体とともに加速度運動する観測者の立場に立ち、力Fとつりあう慣性力-maを考えるのだ。

これで仮想仕事の原理が使える。
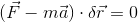
このように、慣性力を考えた場合も含めて仮想仕事の原理が成り立つことを、ダランベールの原理という。この式は、成分ごとに分けて表せば

となり、加速度運動をしている物体についての問題も、ラグランジュの未定乗数法を用いて、

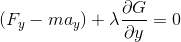
の2式によって解けることが予想できる。これらは、運動方程式を思い出して、


という形の方が覚えやすいかもしれない。
(例)
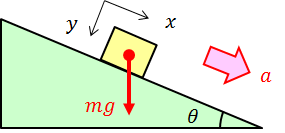
それではダランベールの原理が成り立つことを確かめよう。摩擦の無いなめらかな斜面を物体が滑り降りている状況を考える。いま、この物体は
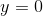
という束縛条件下で運動しているので、束縛条件Gは

である。すると、

だから、ラグランジュの未定乗数法より、
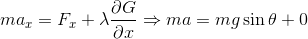
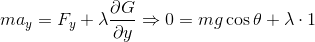
という2式が作れる。1つ目の式を加速度aについて解けば、

となり、普通の運動方程式の解と等しくなっていることが分かる。また、2つ目の式から、
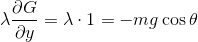
を求めることができる。これは垂直抗力という名の束縛力である。
一般に、
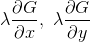
は束縛力の成分表している。束縛力を考えることなく式を立てることができることが仮想仕事の原理の利点であったけれど、実は、こうして求めることもできるのだ。

