フーリエ変換
地震波はさまざまな振動数の波が重ね合ってできている。そこで、どの周波数の波がどれだけ含まれているのかを知るために、元の波形(位置や時間の関数)を周波数の関数に書き変えたりする。この作業をフーリエ変換という。
フーリエ級数展開
-π~πごとに同じ形を繰り返す周期関数f(x)がある。これを、


と表す方法をフーリエ級数展開といい、cやa1,a2,b1,b2などをフーリエ級数という。
それではフーリエ級数を求めていこう。
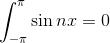
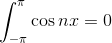
であることに気を付ければ、両辺を-π~πの範囲で積分することでまずはcが求められる。
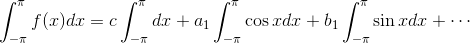
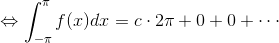

次に、
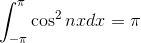


であることに注意して、f(x)の両辺にcos xを掛けて積分すると、



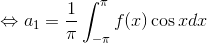
a1を求めることができる。同様に、

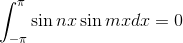
であることに注意して、f(x)の両辺にsin xを掛けて積分すると、
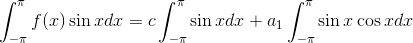

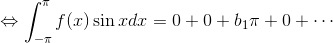

b1を求めることができる。a2,b2,a3…についても同様に計算していくと、フーリエ級数an,bnは、
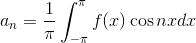
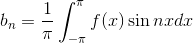
ということになる。
ここで、n=0のときのa0より、
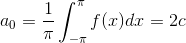
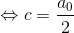
ということが分かる。そこで、今後はf(x)を
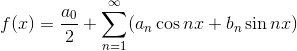
と表現することにしよう。Σ(シグマ)記号は、n=1~∞の数字をすべて足し合わせるということを意味している。
複素フーリエ級数
sinとかcosを使って表すとどうしても長くなってしまう。どうにかしてこれを短くする方法はないだろうか。そこで、複素数を利用する。オイラーの公式より、

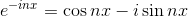
という2種類の関係式が分かる。これらの式から、

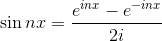
を求めることができるので、これを使ってf(x)を書き変えると、
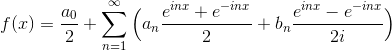
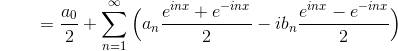
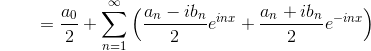
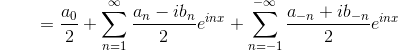
ここで、

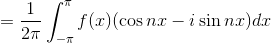
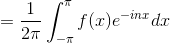

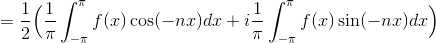


より、
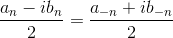
となっていることがわかる。そこで、

とおこう。すると、

だから、f(x)は、

と表すことができる。
-π~πからの拡張
これまでは-π~πの周期関数を考えていたが、今度はこれを-1~1だとか-10~10のような周期関数に拡張して考えよう。周期関数f(x)の範囲を-L~Lとすると、
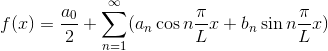
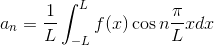
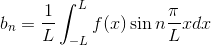
または

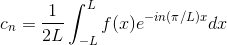
と、まとめることができる。
フーリエ変換
これで、-L~Lの周期関数を表すことができるようになった。ところで、これを-∞~∞の範囲に拡張できれば、どんな関数にも対応できるようになるはずだ。とりあえず、
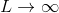
という方向で考えていく。いま、
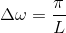
とおいて上の式を書き変えてまとめると、



となる。ここで、nΔωはn番目のωという意味だから、これをωnと書き変えることにしよう。
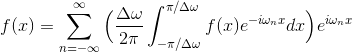

長くてややこしいので、
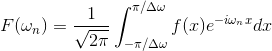
とおけば、f(x)を
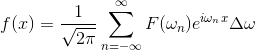
と書き変えることができる。L→∞のときΔω→0であり、このとき、シグマ以降は横軸ω、縦軸F(ω)eiωxのグラフの面積を表しているわけだから、積分形式で書き直すことができる。

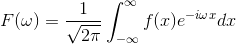
これで、xの関数f(x)をωの関数F(ω)に変換することができた。F(ω)を、f(x)のフーリエ変換という。
