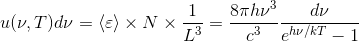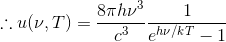プランクの法則
今回は、前回登場したプランクの法則
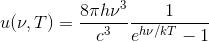
この導出に挑戦してみよう。u(ν,T)は周波数νを持つ電磁波の、単位体積あたりのエネルギーのことであり、これをエネルギー密度と呼ぶ。
電磁波の平均エネルギー
統計力学の考え方によると、振動する物体がエネルギーεを持つ確率は、次のように与えられるので、

ここで、「電磁波はとびとびの値しか持つことができない」というプランクの量子仮説を、次のように表すことにし、
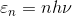
これをもとの式へ代入しよう。

するとこの式は、「電磁波がエネルギーnhνを持つ確率」ということになる。プランクは、空洞の内壁が放出するエネルギーがとびとびの値しか取れないと考えたようだが、今回は電磁波がとびとびの値しか取れないとして作業を進めていくことにする。
ここで、たくさんのサイコロの出た目の平均値は、目の値とその確率の積を、目の数だけ足し合わせることで求められるので、これと同様に考えると、電磁波の平均エネルギーが次のように表されることが分かる。
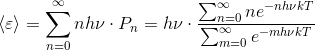
ややこしいので
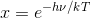
とおけば

のようになる。分数部分の分母をSとすると、
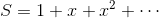
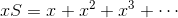
であり、x<0だから
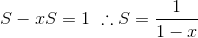
が得られる。続いて分子をS'とすると、
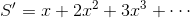
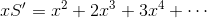


が得られるから、

となる。あとは、この平均エネルギーに周波数νを持つ電磁波の数を掛けてやることで、周波数νを持つ電磁波のエネルギーを求めることができる。
電磁波の数

空洞放射を考えると、電磁波は、空洞の中で図のような定常波を作っていると考えられる。この定常波の数を数えよう。一辺Lの立方体の形をした内壁を考えると、電磁波の周波数は光速cを用いて
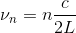
と表せる。弦の振動や気柱の振動を思い出そう。
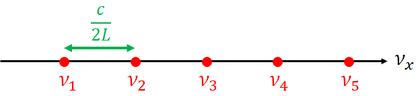
この式は、周波数軸上で、電磁波の周波数は間隔c/2Lでとびとびに存在していることを示している。このことは、x軸方向の定常波だけでなく、y軸方向、z軸方向も同様である。
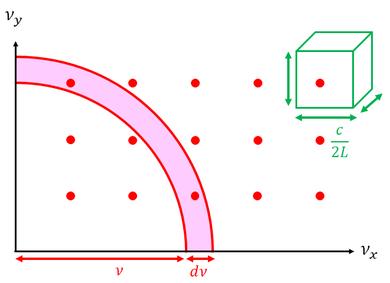
ただし、n>0、ν>0なので、周波数の成分すべてが正の値の空間上にしか、この点は存在できない。
周波数空間上で、原点からの距離ν~ν+dνの球殻に含まれる点の数を数えよう。この球殻の体積は4πν^2×dνだから、この体積を1辺c/2Lの立方体の体積で割ることで、数が求められる。

1/8になっているのは周波数成分が正の値にしかなれないからで、2が掛かっているのは、例えばx軸方向の定常波では、電磁波の振動方向がy軸方向とz軸方向の2種類存在するからである。
プランクの法則
電磁波の平均エネルギー<ε>と、電磁波の数Nが求められたので、この積を計算し、空洞の体積L^3で割ることによって、周波数νの電磁波のエネルギー密度u(ν,T)を求めることができる。