連続体の変形 ←
弾性体の振動~地震波~
P波とS波

変位ベクトルなどのベクトル場は、回転しないが発散する場と、発散しないが回転する場に分類することができる。これをヘルムホルツの定理という。ナビエの方程式
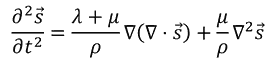
の両辺の発散を取ると、
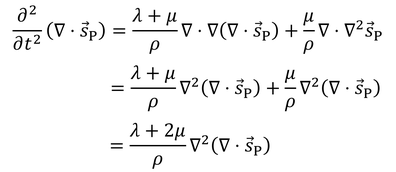
となるので、
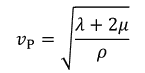
とおくと、
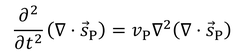
波動方程式を満たすことがわかる。これは膨張・収縮する波を表しており、膨張波または縦波と呼ばれている。s_Pは回転しないので、
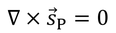
が成り立っている。続いて、ナビエの方程式の両辺の回転を取ると、
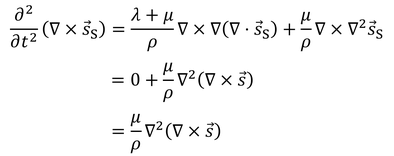
となるので、
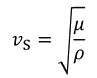
とおくと、
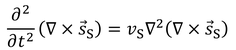
波動方程式が成立していることがわかる。この波を回転波または横波と呼ばれている。s_Sは発散しないので、
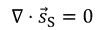
が成り立っている。
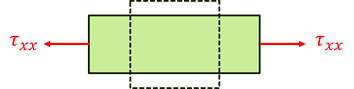
ここで、弾性体の両端に引っ張り応力を加えたときの話を思い出そう。応力τとひずみεの間には、
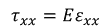
という関係がある。Eはヤング率だった。また、応力は2種類のラメ定数λ,μおよびポアソン比σを用いて、
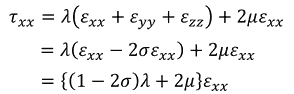
と表すことができる。これらより、E,λ,μ,σの間には、
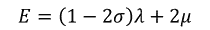
という関係があることがわかる。さらに、この状況ではy方向の応力が0だから、
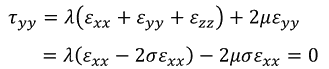
より、
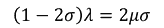
という関係があることが分かる。よって、2種類のラメ定数をヤング率とポアソン比を用いて書くと、
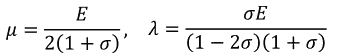
となる。これを使うと、P波とS波の速さの比が、
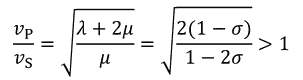
ポアソン比を用いて表されることが分かる。この式より、縦波のほうが横波よりも速いことが分かる。
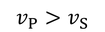
地球を半無限弾性体と考えることができる。地中で生じた岩石の破壊(地震)によって生じた地震波には、初めに地表に達するP波と、P波に続いて到達するS波がある。P波が縦波、S波が横波であり、P波の速さは約6.5km/s、S波の速さは約4km/sだから、このときポアソン比は約0.2となる。これは岩石の測定値とほぼ等しい。
レイリー波

地表面を伝わる地震波を表面波という。表面波には、鉛直面内で楕円を描くレイリー波と、水平面上を進行する横波のラブ波がある。先にレイリー波から見ていこう。x方向に伝わるレイリー波を縦波成分s_Pと横波成分s_Sに分類し、

と表す。深さ方向にz軸を取り、y方向の変位はなく、y方向に波は伝わらないとすると、

であることに注意すると、縦波についての波動方程式は、
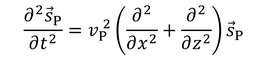
だから、ここへs_Pの式を代入して計算すると、

となり、

となるから、深さ方向への振幅の形f(z)が、

と求められる。eの指数は+Kzも解ではあるが、深部ほど振幅が増すことになるため不適である。深部で振幅が0になるようにeの指数を-Kzにしている。ここで、

より、レイリー波の速さがP波よりも遅いことが分かる。

同様に、横波成分についても考えると、f(z)は
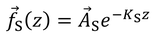
と表され、
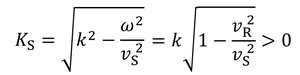
より、レイリー波の速さはS波よりも遅いことが分かる。

ここまでの議論を踏まえてレイリー波の変位を成分表示すると、

となる。次はこれらの係数Aの関係を求めよう。縦波成分の回転は0だから、
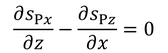
であり、ここへ変位を代入して微分を行うと、

より、

を得る。続いて横波の発散が0であることから、

ここへ変位を代入して計算すると、

だから、
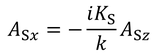
を得る。変位の成分を書き直すと、

となる。ここで、地表面で応力が0であることを使って、残りの定数の関係を考えよう。x方向の応力は、

z方向の応力は、

ここで、ラメ定数をP波とS波の速さで表すと、
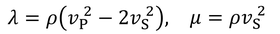
になるから、

が得られ、さらに
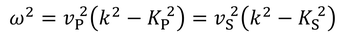
を使うと、
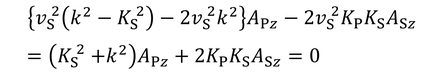
となる。係数を使った2式をまとめると、
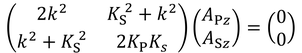
になるが、2つの係数Aが0以外の値を持つには、前の行列式が0であればよい。
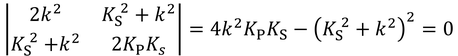
この式を、

と表し、2乗してK_PやK_Sを書き換えて、
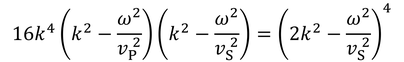
レイリー波とP波とS波の速さの関係が得られる。
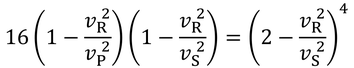
P波の速さを6.5km/s、S波の速さを4m/sとすると、レイリー波の速さは3.6km/sになる。ややS波よりも遅いのだ。
ラブ波
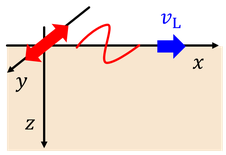
次はラブ波について見ていこう。振動はy方向だから、
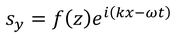
と表し、
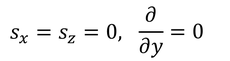
であることに気を付けて横波の波動方程式
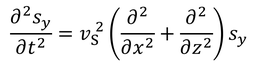
に代入して計算すると、
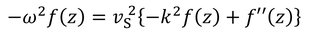
になり、これを
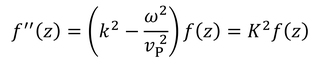
と表すことで、
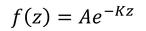
を得る。また、

より、ラブ波の速さがS波の速さよりも遅いことが分かる。

これで、ラブ波の変位が

になるから、これを使って、地表面で応力が0になることを使うと、

K=0になる必要があることが分かる。つまり、変位が

と表せ、地中が全く振動しないことを意味する。
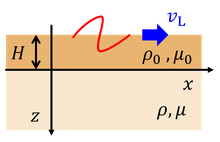
さすがにおかしいので、物理的性質の異なる、表面と内部の2層を伝わるラブ波を考えよう。柔らかいマントルの上に硬い地殻が乗っていることに対応している。境界面をxy平面に合わせると、下層の変位は、
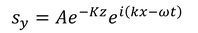
と表される。上層の変位は、
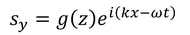
とおいて、波動方程式に代入してg(z)を求めよう。上層でのS波の速さをv_S0とすると波動方程式は
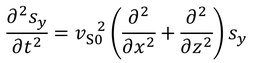
だから、
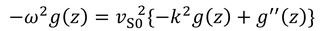
となる。g(z)とその2階微分の関係が、

になるので、
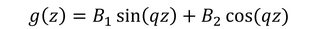
を得る。深さに従い振幅が減少する場合は、1層のみで考えた時のように地中でラブ波が生じないことになってしまうため、上層では振幅が三角関数で表されているものとした。定数qが、
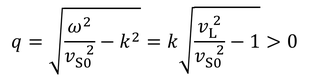
であることから、ラブ波の速さv_Lは上層でのS波の速さよりも速いことがわかった。

g(z)の結果を用いて上層の変位を書き直せば、

となる。続いて係数A,B_1,B_2の関係を考えよう。y方向の応力が、

地表面(z=-H)で0であることから、
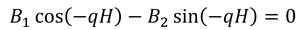
より、

を得る。次は、2層の境界で変位が等しいことを使って、
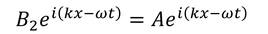
より、
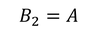
を得る。最後に、2層の境界で応力

が等しいことを使って、

より、

を得る。この式は、A=B_2であることを使うと、
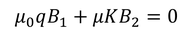
となる。B_1とB_2を使った関係をまとめると、

と表せて、B_1とB_2が0以外の値を持つためには、

であればよく、

が得られる。qとKを戻すと、
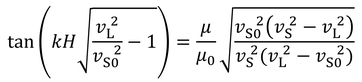
となる。これがラブ波の速さを求める式である。レイリー波と異なり波数kに依存しているので、伝播に従って波が分かれていく。このような性質を持つ波を分散のある波と呼ぶ。