ボース分布
1つの状態に1つしか収まることができないのがフェルミ粒子、いくらでも収まることができるのがボース粒子であった。今回はボース粒子の統計的な性質を調べていこう。
ボース分布
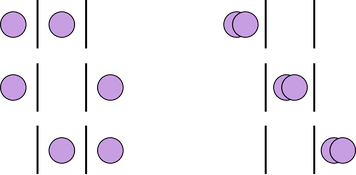
ボース粒子は1つの状態に複数収まることができるため、例えば3つの状態に2つの粒子が収まるパターンは、上の6通りがある。左の3通りはフェルミ粒子のときと同じだが、右の3通りはボース粒子特有の性質によるものである。考え方は、区別できない2つの粒子と2つの仕切りの並べ方を考えればいいから、
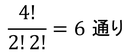
と計算できる。同様に、Δ個の状態にn個の粒子を収めるパターンは、Δ-1個の仕切りとn個の粒子を並べる方法を考えて、
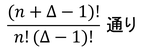
と分かる。これをj番目のエネルギーを持った粒子の微視的状態数と考え、すべてのエネルギーのときをかけ合わせることで
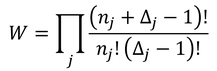
ボース粒子が取り得る微視的状態数Wが得られる。熱平衡時にはこれが最大になると考えられる。ミクロカノニカルアンサンブルの方法で求めることにしよう。計算しやすいようにlogWを考える。
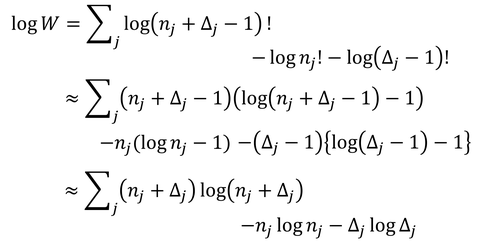
スターリングの公式(logN!≒NlogN-N)を考え、Δとnは1に比べて非常に大きいとした。粒子数とエネルギー一定の下でこれが最大になるような粒子の分布n1,n2,…を求める。logWの変分を考え
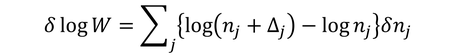
ラグランジュの未定乗数法を用いる。
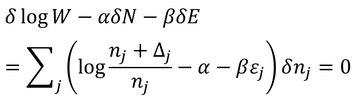
( )の中が0となるようなnjを求めることで、

熱平衡時の粒子数の分布が得られる。これを「ボース分布(ボース・アインシュタイン分布)」という。また、Δで割ることで状態ごとの分布も得られる。

αとβは前回と同じ計算で同じ結果が得られる。
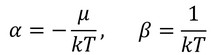
これにより、
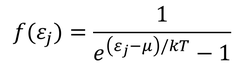
を得る。
光子の例

エネルギーを連続と考えたときのボース粒子の確率分布

を「ボース分布関数」と呼ぶ。
ボース粒子の代表例が光子である。光子を温度T,体積Vの空洞に閉じ込める。光子は空洞の内壁に吸収されたり、逆に放出されたりしているため、数が変化している。自由エネルギーが

と表せることを思い出せば、TとVが一定のとき、
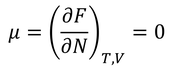
となる。これが0になったときが熱平衡である。つまり、μ=0のときのボース分布関数

これが光子の確率分布である。光子のエネルギーをℎνとした。
ボース・アインシュタイン凝縮
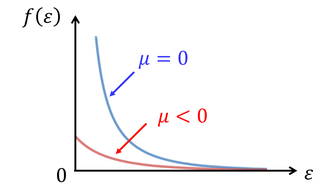
ボース分布関数に現れる化学ポテンシャルμは、μ≦0を満たす。仮にμ>0とするとε<μの範囲でe^((ε-μ)/kT)<1であり、存在確率が負の値となってしまうためだ。

絶対零度のとき、フェルミ粒子はエネルギーの低い状態から順番に収まっていくが、ボース粒子は同じ状態に複数の粒子が収まれるので、エネルギー0の状態にすべての粒子が収まることになる。このように、低温で多くの粒子がエネルギー0の状態に落ち込む現象を「ボース・アインシュタイン凝縮」と呼ぶ。
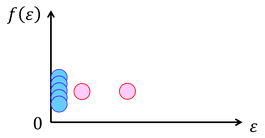
全粒子数Nを、エネルギー0の基底状態N0と励起状態N'に分けて考える。
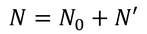
N0はボース分布関数をε=0として
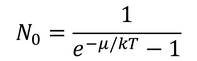
得ることができる。N'は、状態密度
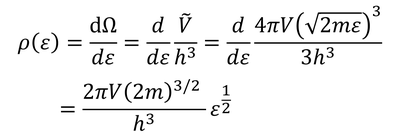
に分布関数f(ε)を掛けて、すべてのエネルギー0~εについて足し合わせることで求められる。
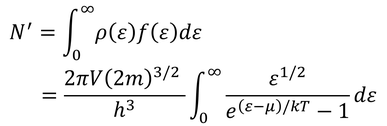
ここで、
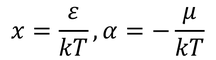
とおくと
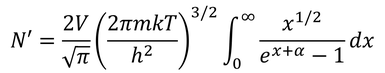
となる。さらに
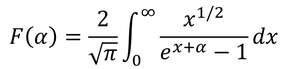
とおくことで
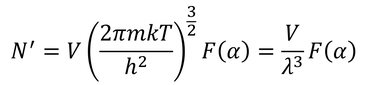
を得る。
ところで、ボース・アインシュタイン凝縮が生じ始める温度Tcを「臨界温度」と呼ぶことにしよう。N0の式を見ると、T→0のときN0が0よりも大きな数値を取るためにはμ=0でなければならないことが分かる。つまり、T≦Tcのときμ=0である。
T=Tcのとき、μ=0でありα=0である。全粒子数Nおよび励起状態の粒子数N'が等しいとすると、

となる。
T>TcのときもN=N'となるときがあり、
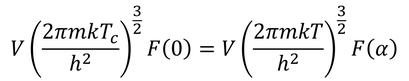
という関係にある。
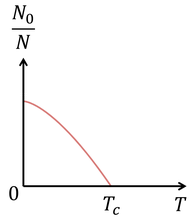
T<TcのときはN0>0だからN>N'である。μ=0に注意して
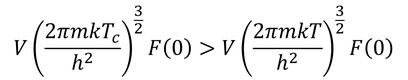
という関係にある。両辺の比は、
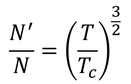
だから、NとN0の比も
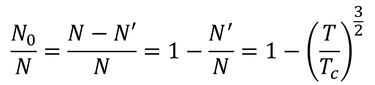
このように計算できる(上図)。
4,2ヘリウムはボース粒子であり、4.2ケルビンで気体から液体に、2.17ケルビンで粘性のない「超流動状態」になる。超流動状態となった液体ヘリウムは内壁をよじ登るなどの面白い性質を示す。これは、ヘリウム原子の多くがボース・アインシュタイン凝縮を起こしており、それ以上エネルギーを失わないエネルギー0の状態であるためであると考えられている。
光子はボース・アインシュタイン凝縮を起こさない。ボース・アインシュタイン凝縮は温度が下がって励起状態になれなくなった粒子が基底状態に落ち込む現象であるが、その前に光子は内壁に吸収されてしまうのだ。
量子統計と古典統計
フェルミ分布関数とボース分布関数は、
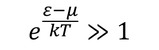
のとき
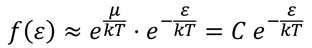
となる。これは、ボルツマン分布(マクスウェル・ボルツマン分布)である。粒子が波動の性質を持っているとき、その波長をドブロイ波長と呼び、
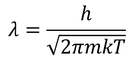
と表される。少し上で、N'の式変形に使用しているので見返してみて欲しい。温度Tが高いとドブロイ波長は小さくなり、古典的な性質が弱くなる。すなわち、温度が十分に高く、粒子の間隔がドブロイ波長に比べて無視できるほど広ければ、量子的な性質が失われ、古典的な統計であるボルツマン分布と見なせるようになるということなのだ。
