測地線方程式
一般相対性理論における基礎方程式は2つある。1つめは、重力によって曲がった時空内を、物体や光がどのように進むのかを表す方程式で、「測地線方程式」と呼ぶ。物体や光は、曲がった時空を「まっすぐ」進んでいると見なすのだ。それでは、導いていこう。
一般座標変換
4次元時空における距離は世界間隔で表され、特殊相対性理論では
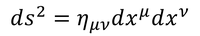
と表された。このように表される時空をミンコフスキー時空と呼び、ηをミンコフスキー計量と呼ぶ。ηの成分は定数で、位置によって値は変わらない。しかし、重力によって曲げられた時空では計量は位置の関数となる。これをg(x)と書くことにし、曲がった時空での世界間隔を、
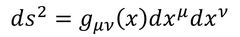
と表す。計量gにはηと同じく対称性があり、添え字を入れ替えても変わらない。

慣性系をつなぐローレンツ変換によって物理法則が変化しないことを、特殊相対性原理と呼び、これが特殊相対性理論の基礎になっていた。同様に、加速度系を含めても物理法則が変化しないような座標変換を考えることにしよう。これを、「一般座標変換」と呼ぶ。
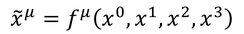
ここで、全微分を
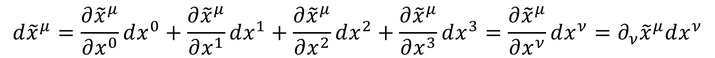
と表す。最後の表し方は、このページの後半に使用するので覚えておいてほしい。
いま、全微分と同じように
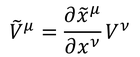
と変換される量Vを「ベクトル」と定義し、
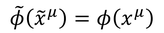
のように一般座標変換によって変化しない量Φを「スカラー」と定義する。また、いま定義したベクトルを特に「反変ベクトル」と呼び、
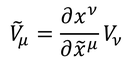
のように、反変ベクトルと係数が逆数の関係にあるベクトルを「共変ベクトル」と呼ぶ。
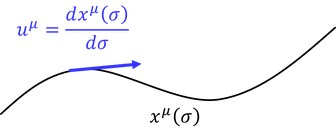
ベクトルの具体例を紹介しよう。曲面x(σ)に接する接ベクトルuを一般座標変換すると、
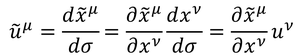
このように反変ベクトルの変換性を満たす。よって、接ベクトルは反変ベクトルであると言える。
続いて、スカラーの微分
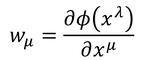
を一般座標変換すると、
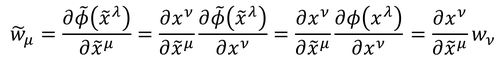
このように共変ベクトルの変換性を満たす。よって、スカラーの微分は共変ベクトルである。
続いて、ベクトルVとWの内積を

と定義する。ベクトルの内積を一般座標変換すると、

となる。変化していないので、ベクトルの内積はスカラーであることが分かる。ここで、

はクロネッカーのデルタである。 また、クロネッカーのデルタの一般座標変換は

となる。これは、ベクトル2つ分の変換性を持っている。このような量を、ランク2の「テンソル」と呼ぶ。特に、クロネッカーのデルタのように、共変ベクトルと反変ベクトルの両方の変換性を持つテンソルを「混合テンソル」と呼ぶ。
共変微分と平行移動
ベクトルの微分
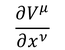
を一般座標変換すると、

第1項だけなら混合テンソルの変換性を示しているが、第2項というおまけがくっついているため、テンソルの変換性を示していないことになる。微分
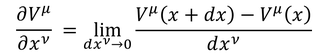
は2点間のベクトルの変化を考える操作であり、2点でそれぞれ一般座標変換するため、テンソルにの変換性を示さないのだ。

そこで、位置xにおけるベクトルV(x)を、位置x+dxまで平行移動して、平行移動したベクトルと、元からその位置にあるベクトルV(x+dx)との変化を考える新しい微分を定義する。
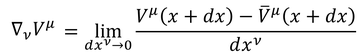
これを「共変微分」と呼ぶ。
共変微分のポイントは平行移動である。平行移動分は元のベクトルV(x)および座標間隔dxに比例するから、
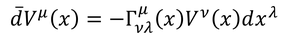
のように、接続係数Γを用いて表現できる。すると、平行移動後のベクトルは
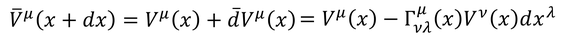
となるので、反変ベクトルの共変微分は接続係数Γを使って
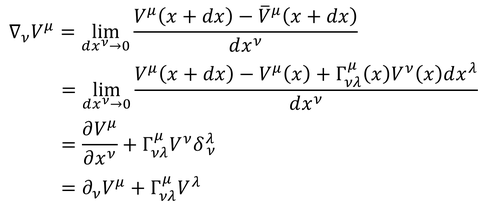
と表されることが分かる。
共変ベクトルの共変微分は、内積の共変微分から得られる。
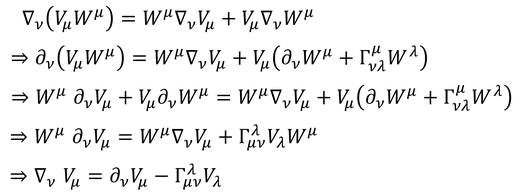
反変ベクトルの共変微分は普通の微分に接続係数Γの項が加わり、共変ベクトルの共変微分は普通の微分から接続係数Γの項を引く形になっている。テンソルの共変微分のルールもこれと同じである。

このように、上付きの添え字に対応する項を加え、下付きの添え字に対応する項を引けばよい。
では、接続係数を求めよう。ベクトルを曲面に沿って平行移動させたとき、その長さは不変として
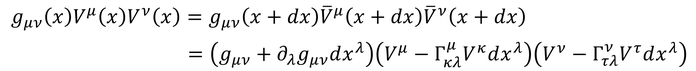
という関係が成り立つ。計量gはテイラー展開している。微小量dxの2乗以降を無視すれば、

となる。この式が恒等的に成り立つためには、カッコの中身が0であればよい。

添え字を入れ替えた式を2つ用意し、

3式を足し合わせると、
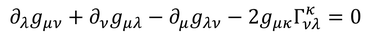
を得る。全体に添え字が上付きの計量を掛けて2で割ることで、

こうして、接続係数を得ることができる。計量を用いて導出される接続係数を、特に「クリストッフェル記号」と呼ぶ。平坦なミンコフスキー時空では、計量の微分が0だったから、クリストッフェル記号も0になる。
測地線方程式
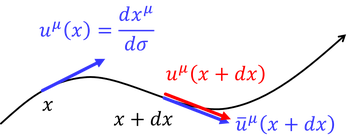
曲がった時空を「まっすぐ」進むとはどういうことだろうか。ここでは面の接ベクトルを考える。面が平坦であれば、接ベクトルがずっと変化しないことがイメージしやすい。曲面の場合は、曲面に合わせて平行移動してやって、

これが位置x+dxの接ベクトルと一致すると考えればよい。
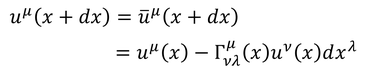
ここで、ベクトルの差をduと表し、
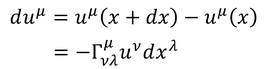
両辺をパラメータの変化dσで割ってやれば、

を得る。これを「測地線方程式」と呼ぶ。特に、パラメータσを固有時τにとると
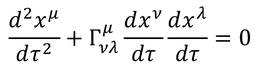
となるが、平坦な時空であればクリストッフェル記号が0だったから、この式は
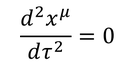
となる。つまり、4元速度uが

変化しないことを表している。時空を物体がまっすぐ進むイメージに当てはまっている。
