双子のパラドックス
動いている慣性系の時間は、基準となる慣性系の時間に比べて遅れてゆっくりと進む。この現象は、立場を逆にさせても成り立つ。すなわち、相手からすると、こちらの時計が遅れて進んでいるように見えるのだ。
双子のパラドックス

地球に双子の妹を残し、姉が光速の99.5%の速さで宇宙旅行へ出かけ、半年後にUターンして地球に戻ってきたとする。動いている慣性系の時計が遅れるのだから、妹からすればロケットに乗っていた姉の時計が遅れている。逆に姉からすれば地球が動いているわけだから、地球に残った妹の時計の方が遅れている。姉が地球に戻って来たとき、姉妹の年齢はどのような関係になっているのだろうか。これを「双子のパラドックス」という。
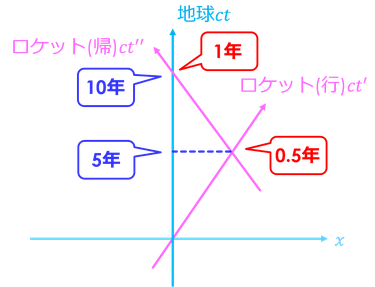
この問題を姉・妹の2つの慣性系と考えると誤ってしまう。姉のロケットは行きと帰りで異なる運動をしているため、3種類の慣性系を考える必要があるのだ。時空図は上のようになる。
姉の時間がロケットの中で0.5年経過したとき、妹の時間は
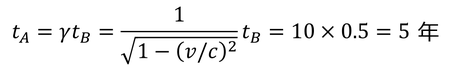
その10倍の5年が経過している。その後、姉は向きを変えてもう0.5年かけて地球に戻ってくる。その間に地球ではもう5年が進むため、姉が1年かけて地球に戻って来たとき、妹の時間は10年経過していることになるのだ。
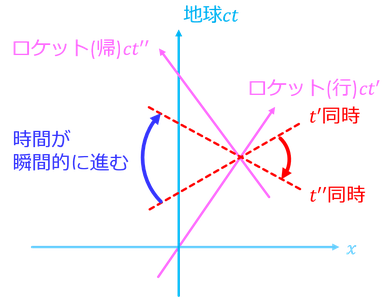
これは次のように説明できる。姉がUターンする直前までは、時間の遅れはお互いさまで、妹の時間が0.05年経過したとき、姉の時間はその10倍の0.5年が経過していたりする。しかし、Uターンして別の慣性系に姉が飛び移った瞬間、「同時」が急激に変化するのだ。そのとき、地球の時間が瞬間的に進むことになる。この現象によって、パラドックスが解消されるのだ。
速度の合成
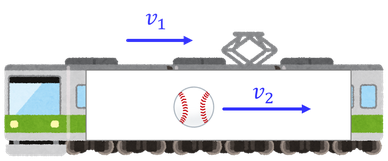
次はこのような状況を考えてみよう。地上に対して速度v1で運動する電車の中で、電車に対して速度v2でボールを投げた。地上から見たボールの速度v3はどのように表されるだろうか。
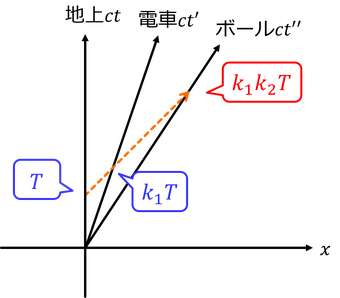
時空図を書いて考える。地上から電車内の観測者に向かって地上の時間でT秒間光を送ったとする。この光を電車内の観測者は、電車内の時間でk1T秒間受け取ることになる。

電車内の観測者は、地上から光を受け取ったらすぐにボールへ光を送る。すると、この光をボールが受け取った時間は、ボールの時計でk1k2Tとなる。
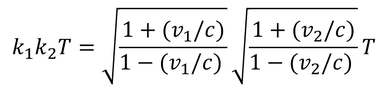
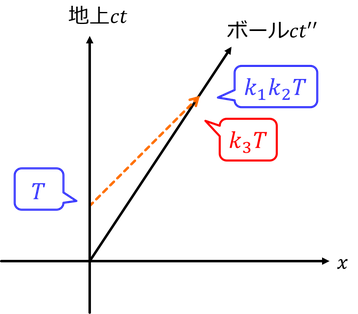
いまの状況は、地上から直接ボールに光を送っても同じである。ボールは光をk3T秒間受け取ることになる。地上に対するボールの速度をv3とすると、
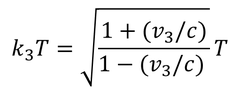
ボールの時間k1k2Tとk3Tは同じものだから、

であり、この式より
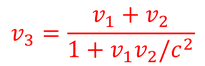
を得る。これが、速度v1とv2の「合成速度」である。この式は、v1やv2が光速cに対して非常に小さいとき、すなわち
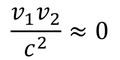
のとき
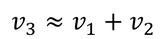
このように、高校物理でおなじみの合成速度の式になる。
ところで、合成速度の式でv1やv2が光速cに等しいとき、高校物理の式であれば合成速度は光速を超える場合が生じてしまう。しかし、新しく導いた式であれば、

このように、合成速度は光速cを超えることがない。よって、光が最も速いというきまりが破綻しないのだ。
ローレンツ変換
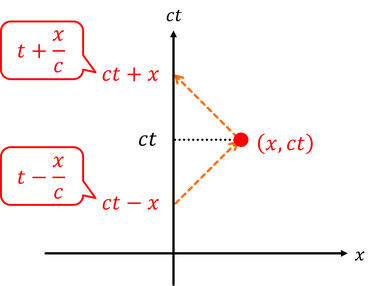
地上の時空図上で座標(x,ct)の観測者に向かってx=0の位置から光を送った。すると、送った時刻はt-x/cになるから、その座標は時間軸上でct-xとなる。また、光を受け取った観測者がすぐに光を送り返したとすると、x=0の位置でこの光を受け取る時刻はt+x/cだから、この座標は時間軸上でct+xとなる。
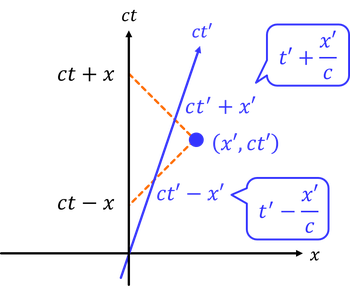
いまのやり取りの間に、地上の慣性系に対して速度vで運動する慣性系を挟む。電車内の慣性系では、観測者がいるのは座標(x',ct')である。地上から放出された光を電車内で中継した時刻は、電車内の時計でt'-x'/cである。また、観測者が地上に向けて返した光を中継した時刻は、電車内の時計でt'+x'/cである。このことから、電車内の慣性系についても時空図を書くことができる。
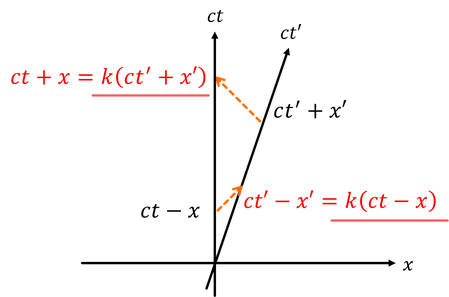
地上から光を送った時刻t-x/cと、電車内でこの光を中継した時刻t'-x'/cの関係は、定数kを用いて
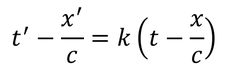
である。この光を受け取った観測者が地上へ送り返した光を電車内で中継した時刻t'+x'/cと、地上でこの光を受け取った時刻t+x/cとの関係も、定数kを用いて

と表せる。この2式より、

を得る。ここで、
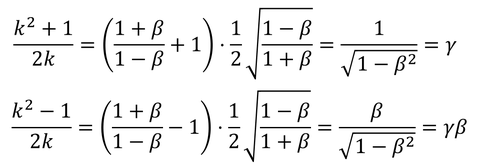
とおくと、

となる。この式はガリレイ変換とは異なり時間を踏まえた座標変換を与える式で、これを「ローレンツ変換」という。
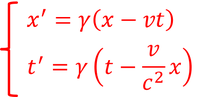
とも表せる。
ローレンツ変換の式を用いて、これまで時空図を使って求めてきた時空に関する関係式を求めることができる。
①合成速度
例えば、地上に対して速度v1で運動する電車があり、この電車に対して速度v2で運動するボールがあるとする。速度v2(=x'/t')は

と書けるから、地上に対するボールの速度v3(=x/t)が
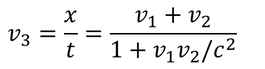
計算できる。上で導出した合成速度を求める式だ。
②時間の延び
また、経過時間Δt’(=t2'-t1')を計算すると、
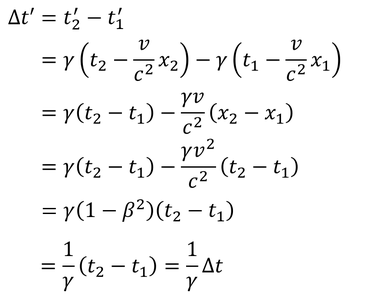
となる。すなわち、
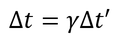
これは、運動している慣性系の時間が延びることを表す式である。
③空間の縮み
また、距離L'(=x2'-x1')を計算してみると、

となる。これは、
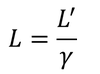
運動している物体の空間が縮むことを表す式である。これを「ローレンツ収縮」という。ローレンツやフィッツジェラルドは、エーテルに対して運動する場合に距離が縮むと考えたが、実際はエーテルなんてなくても、運動している物体の空間が縮むことで成立する式だったのだ。
