E=mc2
核反応などにおいて、原子核の質量が減ることでエネルギーが発生することが知られている。このとき、減少した質量と発生したエネルギーの間には、とある有名な関係が成り立っているのだ。
4元ベクトル
時空図上の座標(ct,x,y,z)を、それぞれxの右上に0~3の添え字を付けて表すことにする。
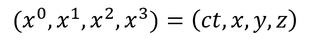
すると、ローレンツ変換は

となる。1つ目の式と2つ目の式の間に対称性があることがよく分かる。また、この式は
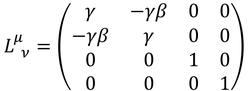
という行列を考えることで、各成分が
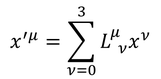
と表される。Σ記号は総和を表すが、今後このような計算が多いので、Σ記号を省略し、

と書くことにする。Lの右下とxの右上にνが付いているが、このように右下と右上に同じギリシャ文字が使われているとき、0~3のときをそれぞれ足し合わせると決めてやる。これを「アインシュタインの縮約記法(規約)」と呼ぶ。
同様の手法で世界間隔も書き変えよう。
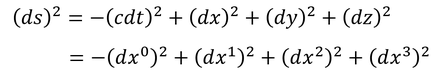
ここで、

という行列を導入すると、世界間隔の2乗は

と表せる。この行列ηは時空における距離を表す目安となるものなので、「計量(メトリック)」と呼ばれる。
x,y,z方向の向きと大きさを持つ量を「ベクトル」というが、今回はそれに時間方向を加えて表した。これを「4元ベクトル」と呼び、
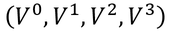
と表し、右上に添え字を付ける。特に、

を「4元位置ベクトル」と呼ぶ。
共変ベクトル
世界間隔をメトリックを使って表したのと同様に、4元ベクトルの内積もメトリックを使って次のように定義する。
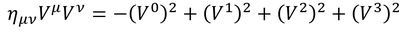
この内積は非常によく使うので覚えておこう。しかし、毎回メトリックを用いるのも面倒なので、時間成分のみ符号を入れ替えた

という4元ベクトルを導入しよう。これを「共変ベクトル」と呼び、右下に添え字を付けて表す。共変ベクトルに対して、右上に添え字を付けて表してきた4元ベクトルは「反変ベクトル」と呼ばれる。共変ベクトルを用いることで、内積が
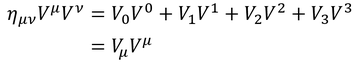
このようにメトリックなしに記述できる。
また、この式から、共変ベクトルと反変ベクトルとの変換は
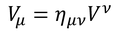
だと分かる。逆の変換にも同じ行列が使用できるが、
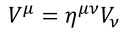
このように、ηの右上に添え字を書くことにする。
世界間隔を共変ベクトルを用いて表すこともできる。

ところで、η_(μν)はη^(μν)の逆行列である。逆行列というのは、掛けたら単位行列Iになる行列のことである。

同じように、ローレンツ変換を表す行列Lの逆行列によって、ローレンツ変換の逆変換が行える。逆行列にはバーを付けて表す。
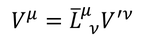
また、同じ逆行列を用いることで、共変ベクトルのローレンツ変換も表せる。

すると、ローレンツ変換後の世界間隔は

のように表せる。ここで、慣性系によって世界間隔は不変に保たれるから、

より

の関係を得る。
特殊相対性原理
反変ベクトルで偏微分した量
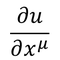
のローレンツ変換を考える。反変ベクトルの微小量dx'のローレンツ変換から
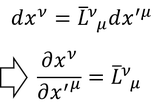
が得られるから、
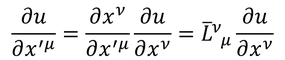
となる。この式は、共変ベクトルのローレンツ変換の関係を満たしている。すなわち、反変ベクトルで偏微分された量は、共変ベクトルである。
この関係を使って、波動方程式

のローレンツ変換を計算しよう。波動方程式は、
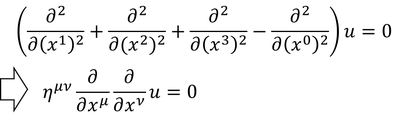
と書き変えられるので、左辺をローレンツ変換すると、
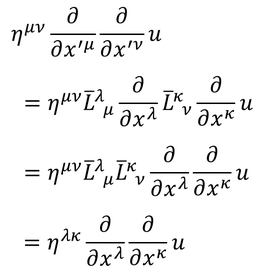
このように、形を変えないことが分かる。
ガリレオの相対性原理はすべての慣性系で運動の法則が成り立ち、ガリレイ変換によって運動の法則が不変に保たれるというきまりであった。これが拡張された「特殊相対性原理」は、すべての慣性系ですべての物理法則が成り立つという内容であった。波動方程式の例のように、特殊相対性原理は、ローレンツ変換によってあらゆる物理法則が不変に保たれると言い換えることもできるのだ。
4元速度
4元位置ベクトルと同様に、「4元速度」を次のように定義する。

τは固有時間である。

これを使って4元速度の各成分を求めてみると、

となる。vは3次元空間における速度である。
4元速度の内積は

となる。
また、「4元加速度」も同様に
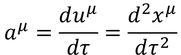
と定義し、運動方程式を
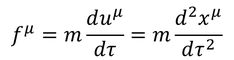
と表す。力fを「4元力」と呼ぶ。4元力は、「4元運動量」

を用いて

と表すこともできる。ここで、
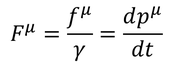
という量を導入すると、1~3成分は3次元空間における力を表す。
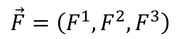
では、0成分F^0は何を表しているのだろう。
uとfの内積が
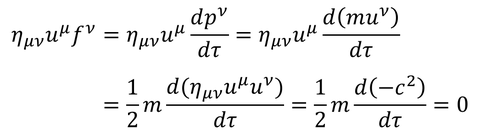
0だから、uとF(=f/γ)の内積も0である。
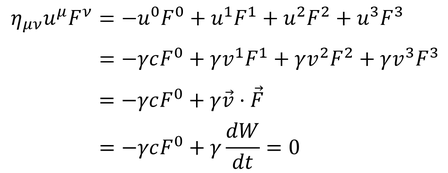
この式から、

Fの0成分は仕事の時間変化に比例することが分かる。この仕事を受け取った物体は、そのぶんエネルギーが増えることになる。つまり、F^0はエネルギーの時間変化なのだ。
ところで、F^0は4元運動量を用いて
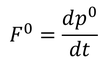
表すこともできた。2式の比較よりエネルギー

を得る。
この式は、特にv=0のときγ=1だから

の関係が得られる。これを「静止エネルギー」という。この式は、4元運動量pの内積から導くこともできる。4元速度の内積は計算してあるから、これを使うと
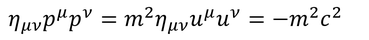
となり、E=cp^0の関係からp^0をEで表せば

となる。この2式より

の関係が得られる。この式より、p=0のとき

になる。
ところで、光はエネルギーE=hνを持った光子はの集まりである。光子の質量をm=0とすると、上の式は

となる。光子がこの運動量を持つことは、実験でも確かめられている。
