自由エネルギー

温度Tの熱源から熱量Qを受け取って状態が変化するとき、

をエントロピーという。ただし、エントロピーの計算は可逆過程Cに沿って行われなければならない。
同じ計算を不可逆過程Xに沿っておこなうと、エントロピーの変化ΔSよりも小さな値となる。

この式はカルノーの定理から導出されたものであり、熱力学第二法則の数式による言い換えだと考えることができる。
ここで、d'Q=0とすればこの式は、

となる。これは「断熱過程において、自然はエントロピーが増大する方へと進む」ことを意味している。これをエントロピー増大則という。
エンタルピー

定積変化のとき、気体がした仕事はW=0だから、熱力学第一法則の式は
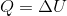
となる。これは「定積変化のとき、加えた熱量Qのぶんだけ内部エネルギーUが増える」という意味だ。
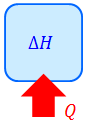
ところで、定圧変化のときも定積変化と同じように「加えた熱量Qと同じだけ物理量Hが増える」と考えてみよう。つまり、

という式を成り立たせるわけ。このHをエンタルピーという。名前は似ているけれど、エントロピーとは別物なので注意。それではエンタルピーはどのような形なのかというと、定圧変化のとき、気体がした仕事はW=pΔVと書けるから、熱力学第一法則の式より

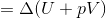
となる。だから、

である。ただし、この式よりも、「Q=ΔH」のイメージの方が大切だ。
自由エネルギー

今度は等温変化について考えてみよう。等温変化のときは内部エネルギーが一定(ΔU=0)だから、熱力学第一法則の式は

となる。これは正しい。しかし、気体の状態が等温であり続けるためには、常に熱平衡が成り立っている必要がある。つまり、可逆過程に限り、上の式が成り立つわけだ。

では、不可逆過程を考慮するとどうなるか。例えば温度Tの熱源から熱量Qを受け取る場合(等温条件下)について考えてみると、熱力学第二法則の式は、熱源が1つしかないから


と表せる。また、熱力学第一法則を使って左辺を書き換えると、


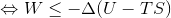
となる。ここで、

とおくと、今の式は

となる。ーΔFはFの”減少量”を表すので、この式は「Fの減少量以上の仕事はできない」ということを意味している。このFを自由エネルギー(ヘルムホルツの自由エネルギー)という。FはUからTSを引いた値になっている。つまり、加熱されて蓄えられた内部エネルギーUのうち、TSは自由に仕事に変えることができないということだ。その意味で、TSの部分を束縛エネルギーと呼ぶことがある。

次は、等温条件に加えて、この変化が定積変化だったとしてみよう。W=0だから、

という関係が成り立っている。等号成立は可逆過程、つまり熱平衡状態のとき。これは、等温・定積条件下で「熱現象はFが減少する方へ向かう」ことを示している。
それでは、等温・定圧条件下だとどのような条件式ができるのだろう。定圧変化ではW=pΔVだから、
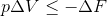

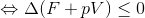


という関係が成り立つ。ここで、

とおくと、今の式は

となる。等号成立は可逆過程、つまり熱平衡状態のとき。これは、等温・定圧条件下で「熱現象はGが減少する方へ向かう」ことを示している。Gをギブスの自由エネルギーという。化学変化などは等温・定圧条件を想定することが多いので、化学の分野ではよく出てくる量のようだ。
マクスウェルの関係式
エントロピーの定義
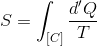
から、


という関係が分かる。また、微小な仕事は「d'W=pdV」だから、微小量に対する熱力学第一法則の式は、
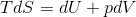

と変形することができる。この式は、内部エネルギーUはSとVで表せるという意味だから、これからはUをS,Vの関数U(S,V)とみなすことにしよう。すると、dUは全微分の公式から

だから、1つ前の式と比較することで、
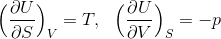
という関係式を導くことができる。ここで、左側の式の両辺をVで、右側の式の両辺をSで偏微分すると、

となるから、この2式を比較すると、
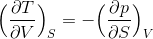
内部エネルギーUと同じように、エンタルピーH=U+pVの全微分dHを考えると、
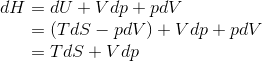
になるから、これからはHをS,pの関数H(S,p)とみなす。すると、

だから、1つ前の式と比較をすることで、
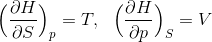
という関係式を導くことができる。ここで、左側の式の両辺をSで、右式の両辺をpで偏微分すると、
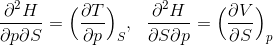
となるから、この2式を比較すると、

今度は、自由エネルギーF=U-TSの全微分dFを考える。
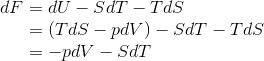
になるから、これからはFをV,Tの関数F(V,T)とみなす。すると、

だから、1つ前の式と比較をすることで、
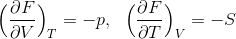
という関係式を導くことができる。ここで、左側の式の両辺をTで、右式の両辺をVで偏微分すると、
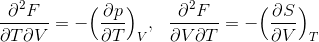
となるから、この2式を比較すると、

今度は、ギブスの自由エネルギーG=H-TSの全微分dGを考える。

になるから、これからはGをp,Tの関数G(p,T)とみなす。すると、

だから、1つ前の式と比較をすることで、
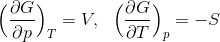
という関係式を導くことができる。ここで、左側の式の両辺をTで、右式の両辺をpで偏微分すると、

となるから、この2式を比較すると、
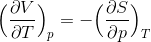
最後に、これまでの結果だけを書き出してみよう。




これらをまとめてマクスウェルの関係式という。この式は、エントロピーSの変化や、エントロピーSに対する変化といった単純には考えにくい量を、そのほかの利用しやすい状態量を使った式に置き換えることができるという意味で価値がある。
