→
いろいろな振動現象
微分の形を含む方程式を、微分方程式という。様々な振動現象を見ていきながら、数学的な手法も学んでいこう。
単振動(調和振動)

はじめは高校物理の復習として単振動を考えよう。質量mの粒子がばね定数kのばねに取り付けられているとき、運動方程式は、

である。加速度は位置xの時間tによる2回微分で表せるから、

と書いてもよい。このように、2回微分を含む微分方程式を「2階微分方程式」という。この式は、角振動数ωを用いると、

となる。この方程式が表しているxは、tで2回微分したら元の形にマイナスを付けた形になるということだ。そのような関数として、


が思いつく。これらを微分方程式の「特解」という。また、いま挙げた特解2つは、一方を定数倍しても他方にぴったり重なることはない。このような関係を「一次独立」という。一般的に、一次独立な特解それぞれの定数倍の和

も微分方程式の解となっている。これを「一般解」といい、2階微分方程式の一般解は、2つの定数を含む。上の一般解は、
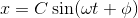
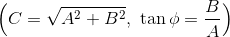
と表してもよい。
減衰振動
続いて、速度vに比例する空気抵抗bvを受ける振動について考えよう。運動方程式は、
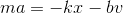
であり、加速度aをxのtによる2回微分で、速度vをxの1回微分で書き直せば、

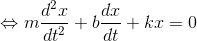
となる。この式の一般解を求めよう。特解として

を考え、これを元の方程式へ戻すことで、
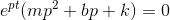
という式が得られる。pは、解の公式から

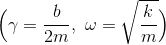
と求められるので、一般解が得られるが、ルートの中身によって運動の様子が異なるので、場合分けをして詳しく見ていこう。

① ルートの中身が正のとき(γ>ω)
pが2つ得られたので、これらを
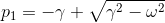

とおいて、定数C1,C2を用いることで、一般解

が得られる。pの値はどちらも負だから、一般解の1項目も2項目も単調に0に近づくようなグラフになる。よって、それらの和も、単調減少となる(上図)。振動せず、ゆっくりとばねが自然長に戻るだけである。これを「過減衰」という。
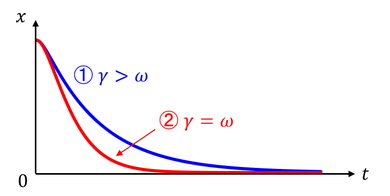
② ルートの中身が0のとき(γ=ω)
pの値は重解となり、

1つしか得られないため、特解が
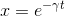
しか求まらない。そこで、
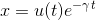
と置いて、そんなu(t)があるかどうか検討してみる。元の微分方程式にこれを戻せば、

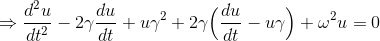
となるが、いま考えているのはω=γのときだから、

となる。このことから、定数α,βを使って、

が得られ、定数が2つ含まれているから、元の微分方程式の一般解
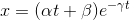
が得られたことになる(上図)。過減衰よりも速く0に収束する。これを「臨界減衰」という。
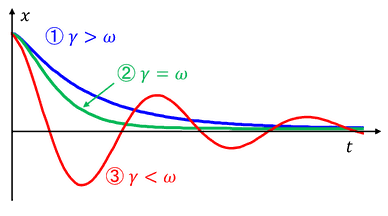
③ ルートの中身が負のとき(γ<ω)
pの値を
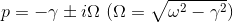
として、定数C1,C2を用いることで、一般解
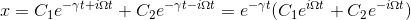
が得られる。この式は、オイラーの公式を用いて、
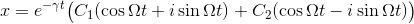


を得る(上図)。振動しながら徐々に0に近づいていく様子が分かる。これを「減衰振動」という。
強制振動
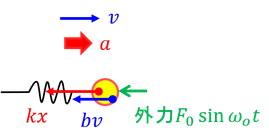
ブランコやヨーヨーのように、外部から周期的な力を加える運動を考えよう。これを「強制振動」という。運動方程式は、


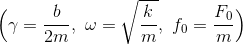
と書ける。
この式は、減衰振動のときの、x、xの1回微分、2回微分のみからなる微分方程式
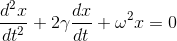
に、それ以外の項が加わった式になっている。減衰振動のときのような、右辺が0の微分方程式を「斉次微分方程式」といい、強制振動のような右辺が0ではない微分方程式を「非斉次微分方程式」という。
一般に、非斉次微分方程式の一般解xは、斉次微分方程式の一般解x_0に非斉次微分方程式の特解x_1を加えたもので表すことができる。
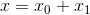
これを確かめるために、非斉次微分方程式の左辺に代入して変形してみる。すると、


このように右辺と一致する。ゆえに、xは非斉次微分方程式の一般解になっていることが確かめられた。
では非斉次微分方程式の特解を求めよう。
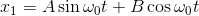
とおき、AとBを求めるために、元の式へ戻して計算する。


sinとcosの係数はそれぞれ0でなければならないから、

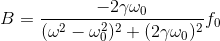
が求められる。特解x_1を、

と表すことにすると、


となっている。
これで、強制振動の一般解が得られた。

時間t→∞とすると、減衰振動の一般解であるx_0は0になるから、このときの振幅はCで与えられる。このCが最大となるのは、

のときである。これは、物体の固有角振動数ωと同じ角振動数ω_0で外力を加えたときが、振幅が最も大きくなることを示している。
