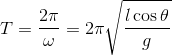力と運動

定積分と極限 ←→ 慣性力

　これまで、等速直線運動や等加速度直線運動などの運動を紹介し、どのような力がはたらいているのかを考えてきた。今回は円運動に焦点を当ててみよう。

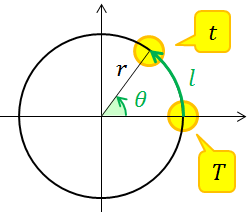
　物体が同じ速さで円周上を進む運動を等速円運動という。等速円運動をする物体の位置は、角度θを使うことで簡単に表すことができる。ただし、角度は30°とか180°といった度数法ではなく、弧度法を使う。弧度法は、半径1の円弧の長さ l〔m〕をそのまま角度 θ〔rad〕として採用したもので、半径がr〔m〕の場合には、

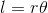
という関係になっている。

　ここで、一定時間 t〔s〕のあいだに回転する角度 θ〔rad〕を角速度と呼び、ω〔rad/s〕で表す。

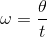
等速直線運動が速度v一定の運動であったのに対し、等速円運動は角速度ωが一定の運動である。このとき、

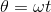
という式が成り立っている。等速直線運動の式「x=vt」と比較をしてみよう。

　また、物体が円周上を一周する時間を周期T〔s〕という。周期は、角度がθ=2π(360°)になるまでの時間だから、

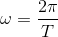
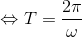
という関係が分かる。

　等速円運動をする物体の速さv〔m/s〕は、円周上の距離l〔m〕を時間t〔s〕で割ることで求めることができる。

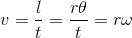
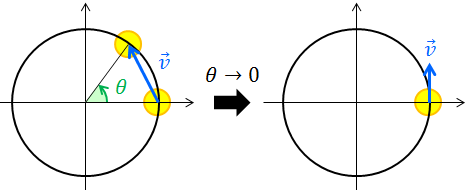
　続いて等速円運動をする物体の”瞬間の”速度を考えてみると、この大きさは、いま求めた物体の速さ

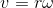
に等しく、向きは”平均の”速度のベクトルについて、θを0に限りなく近づけていけばよいので、上図より円の接線方向であることが分かる。

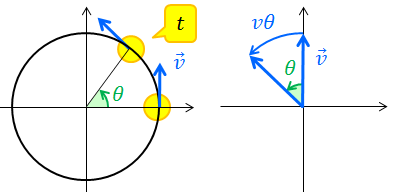
　次は等速円運動をする物体の加速度を考える。「等速」運動なのに加速度が生じるのは、大きさは同じでも速度の向きが変化し続けているからだ。

　まずは加速度の大きさを考えよう。物体の位置がが左上図のように変化したとき、速度ベクトルは右上図のように変化している。だから、加速度の大きさは、速度ベクトルが描く円の弧の”長さ”vθを時間tで割ることで求めることができる。

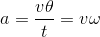
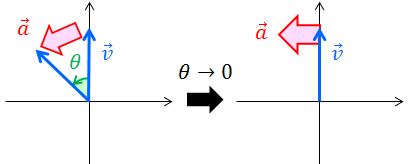
　続いて加速度の向きを考えよう。速度の時と同じように、まずは平均の加速度の向きを考えてθを限りなく0に近づけていけばよい。すると、時刻0のときの加速度はx軸負の向きだということが分かる。

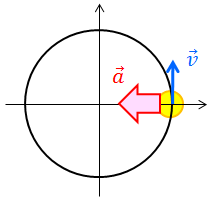
　同じように円周上のすべての位置で考えれば、加速度は常に円の中心を向いていることが分かる。このような加速度を向心加速度という。

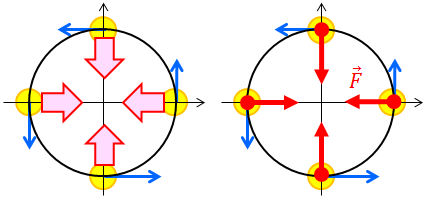
　運動方程式のとき、力Fの向きに加速度aが生じるという話をした。今回の加速度は円の中心向きだから、円の中心向きに何らかの力がはたらいているということになる。この力を向心力という。向心力は、例えば糸におもりを付けてグルグル回すような運動の場合には張力が該当するし、中華テーブルの場合には摩擦力、惑星の運動なら万有引力が該当する。

　ところで、向力加速度の大きさ「a=vω」は、「v=rω」を用いて次のように書き変えることもできるから、

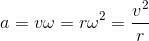
向心力をFとして、運動方程式は次のようになる。

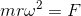
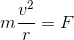
これらを「円運動の運動方程式」と呼ぶ。

問題

次の円錐振り子の周期Tを求めよ。

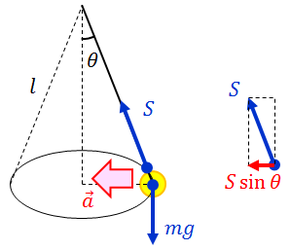
解答

　等速円運動をしている部分で考える。円の半径rは

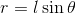
であり、向心力の大きさFは

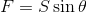
だから、円運動の運動方程式(mrω² = F)は、

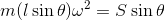
となる。

　また、鉛直方向の力のつり合いより、

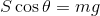
であるから、角速度ωは

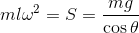
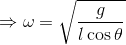
最後に、角速度ωと周期Tの関係式「T = 2π/ω」より、