慣性モーメント
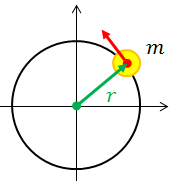
回転運動のしにくさを慣性モーメントといって、質点の場合には
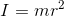
と表される。今回は、大きさを持つ剛体の慣性モーメントの計算をしてみよう。この場合には、剛体を小さな領域に分割して、それぞれの領域における微小な慣性モーメントdIをすべて足し合わせてやればいい。
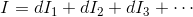
この、「微小量をたくさん足し合わせる」と言う内容は次のように表すこともできる。
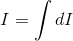
つまり、積分計算をしようというわけだ。
ここで、剛体を微小領域に分けると、それぞれの質量mは微小量dmになる。さらに、これを(密度ρ)×(微小体積dV)という書き方に変えてやると、dIは
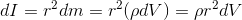
になるので、剛体の慣性モーメントIは

を求めればよいということになる。さあやってみよう!
棒の慣性モーメント
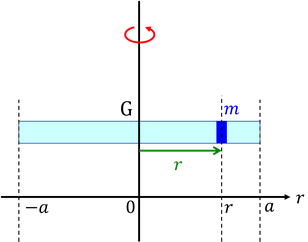
長さ2aの棒を,重心を通過して棒に垂直な回転軸のまわりに回転させるときの慣性モーメントを求めてみよう。回転軸から距離rの位置にある,長さdrの部分に注目する。棒の単位長さあたりの質量(線密度)をρとすると,この部分の小さな慣性モーメントが
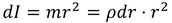
と表されるので、この微小な慣性モーメントを,r=-a~aの範囲で足し合わせることで,
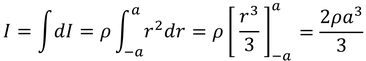
棒全体の慣性モーメントを得る。ここで,棒全体の質量を
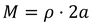
とおくと,
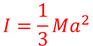
となる。
直方体の慣性モーメント
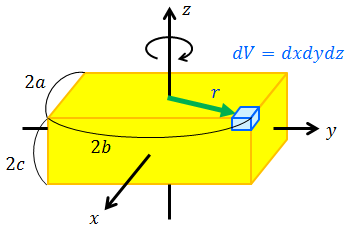
次は図のような直方体を、z軸の周りに回転させるときの慣性モーメントを求めてみよう。rは回転軸からの距離なので、
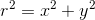
になっている。また、微小体積dVは、軸方向の微小長さdx,dy,dzを使って、
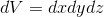
と表されることができるから、微小な慣性モーメントdIは
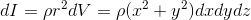
ということになる。あとはこのdIを、
- x = -a ~ a
- y = -b ~ b
- z = -c ~ c
の範囲で計算して足し算(=積分)すればいい。この内容を
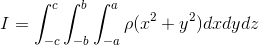
と表記する。この計算を重積分という。計算は内側からおこなうので、まずはxだけを変数と考えて計算して、
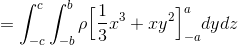
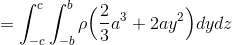
次にyを変数と考えて、
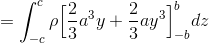
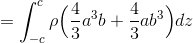
最後にzを変数と考える。
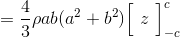
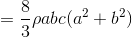
ここで、元の直方体の質量Mは、
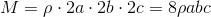
だから、慣性モーメントIをMを用いて表せば、
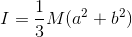
となる。
円柱の慣性モーメント
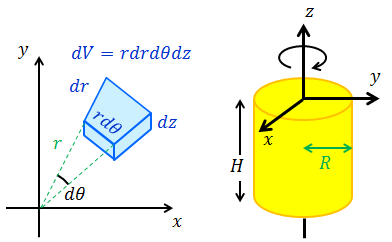
続いて図のような円柱をz軸の周りに回転させるときの慣性モーメントを求めよう。今回、(x,y,z)座標のままでは計算できないので、(r,θ,z)座標を使って計算する。すると、微小体積dVは
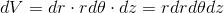
ということになるので、微小な慣性モーメントdIは
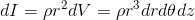
になる。あとは、これを
- r=0~R
- θ=0~2π
- z=0~H
の範囲で積分していけば慣性モーメントIが求められる。
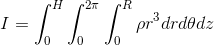
まずはrで積分して、
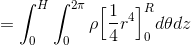
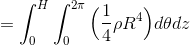
θで積分して、
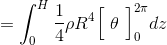
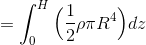
zで積分する。
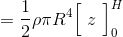
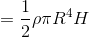
ここで、円柱の質量Mは
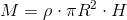
だから、
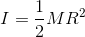
中空円柱の慣性モーメント
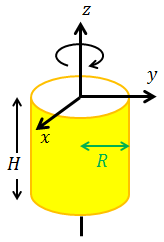
続いて中身が空っぽの円柱の慣性モーメントを求めてみよう。前回との違いは、今回はr=Rが確定しているのでrで積分する必要がないという点だ。すると、微小体積dVは、
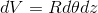
であり、微小な慣性モーメントdIは
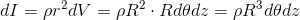
ということになる。あとは、これを
- θ=0~2π
- z=0~H
の範囲で積分すれば慣性モーメントが求められる。
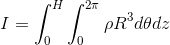
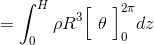
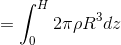
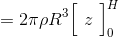
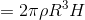
ここで、中空円柱の質量Mは
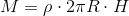
だから、
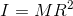
球の慣性モーメント
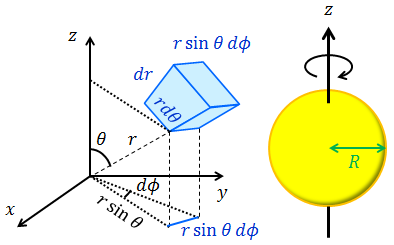
最後に球の慣性モーメントを求めよう。今回は(r,θ,Φ)座標を使う。今回、回転軸からの距離r'は、座標のrとは異なり、
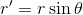
なので注意が必要だ。また、微小体積dVは
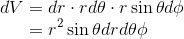
になっているから、微小な慣性モーメントdIは
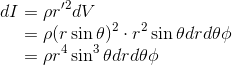
である。あとは、
- r=0~R
- θ=0~π
- Φ=0~2π
の範囲で積分していくことで慣性モーメントIが求められる。
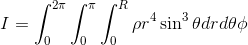
まずはrで積分して、
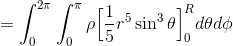
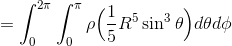
θで積分して、
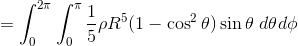
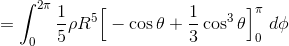
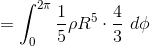
Φで積分すればいい。
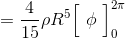
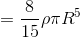
ここで、球の質量Mが
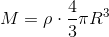
だから、
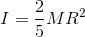
問題
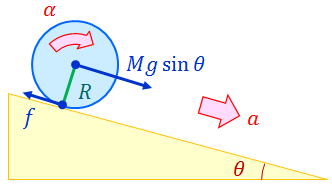
角度θの斜面をすべらずに転がる円柱・中空円柱・球の加速度を求めよ。ただし、前回の問題の結果
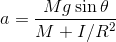
を使ってもよい。
解答
今回計算した慣性モーメントIの結果を使って計算する。
まず、円柱の慣性モーメントは
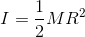
だったから、加速度は
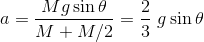
続いて、中空円柱の慣性モーメントは
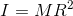
だったから、加速度は
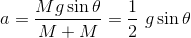
最後に、球の慣性モーメントは
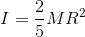
だったから、加速度は
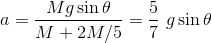
になる。
加速度の大きさが「球>円柱>中空円柱」の順番ということは、斜面を速く転がる順番も同じということ。是非実験してみよう!
