力学的エネルギー保存則
・運動エネルギー
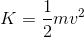
・重力による位置エネルギー
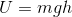
・弾性力による位置エネルギー
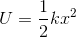
力学的エネルギー保存則
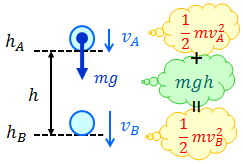
高い位置から落下させた物体が、地点A(高さhA)を速さvAで、地点B(高さhB)を速さvBで通過した。このとき、運動エネルギーと仕事の関係式は、
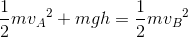
であり、h=hA-hBだから、
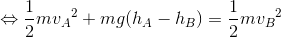
になる。ここで左辺に添え字のAを、右辺にBをまとめよう。
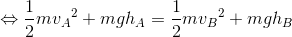
mgh(A)およびmgh(B)は、A地点、B地点の重力による位置エネルギーをそれぞれ表している。よってこの式は、A地点とB地点を比べた場合、明らかに運動エネルギーも位置エネルギーも値が異なっているが、その和は等しいということを示している。ここで
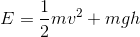


とまとめると、
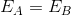
となって分かりやすくなる。
一般的な話をしよう。A地点からB地点まで物体を運んだとき、運動エネルギーKと保存力がした仕事W(A→B)との関係は、
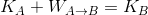
となる。ここで、保存力がした仕事Wはその位置エネルギーの差U(A)-U(B)という形で表せたことを思い出せば、
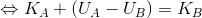
になり、左辺に添え字のAを、右辺にBをまとめると、
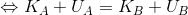
という関係式を導くことができる。ここで
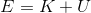
とおくと、
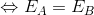
A地点とB地点でEという量が変化しない(保存されている)ことが分かりやすくなる。このEを力学的エネルギーといい、この関係が成り立つことを力学的エネルギー保存則という。
保存力には複数の種類があるが、しばらくは重力と弾性力しか登場しないので、力学的エネルギーEに含まれる位置エネルギーUを「重力による~」と「弾性力による~」だけ考えて、
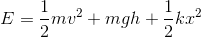
これを力学的エネルギーだと考えてもらってもしばらくは問題ない。今回はこの式を使って話を進めていく。
問題
長さlの糸の先におもりを付け、鉛直方向から角度θの位置から静かに手を放したところ、おもりは円弧に沿って運動した。おもりが最下点に達したときの速さvを求めよ。
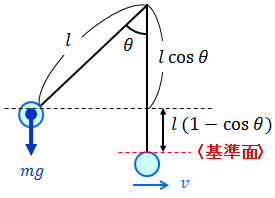
→最下点の位置を重力による位置エネルギーの〈基準面〉とする。
はじめの位置における運動エネルギーは
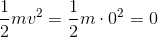
重力による位置エネルギーは
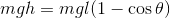
弾性力による位置エネルギーは
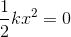
だから、はじめの位置における力学的エネルギーは

である。
次に、最下点における運動エネルギーは
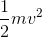
重力による位置エネルギーは
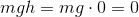
弾性力による位置エネルギーは
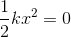
だから、最下点における力学的エネルギーは
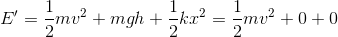
である。
力学的エネルギー保存則(E=E')より、
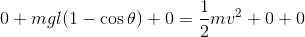
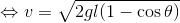
- 力学的エネルギー保存則の式の中に0をたくさん書き込んだ。不要に思えるかもしれないが、運動エネルギーや位置エネルギーを1つ1つ確認しながら式を立てていくという上で重要だ。計算チェックもしやすいので、0を書く癖を付けることをおススメする。
力学的エネルギーと仕事の関係
力学的エネルギー保存則が成り立つためには、実は「保存力以外の力が仕事をしない場合」という条件が必要になる。そこで次は、保存力以外の力が仕事をする場合の関係式を考えてみよう。
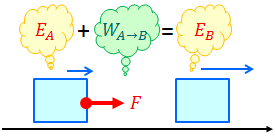
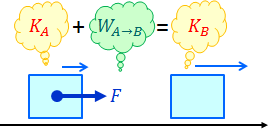
……といっても、新しい話が出てくるわけではなく、運動エネルギーと仕事の関係と同じように、「力学的エネルギーと仕事の関係」を考えればいい。だから、はじめの力学的エネルギーがE(A)で、外部から仕事W(A→B)を受け取り、力学的エネルギーがE(B)になったとすると、
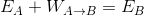
という関係式が成り立っているというわけ。
問題
ばねの端に質量mのおもりをつけ、自然長の長さからゆっくりと下げていったところ、ばねはAだけ伸びてつり合いの状態となった。このとき、外力がした仕事Wを求めよ。
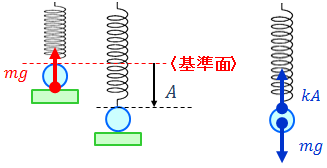
→自然長の位置を重力による位置エネルギーの〈基準面〉とする。
はじめの位置における力学的エネルギーは、
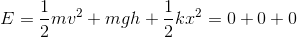
であり、つり合いの状態における力学的エネルギーは
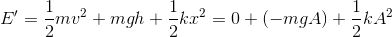
である。
力学的エネルギーと仕事の関係(E+W=E')より
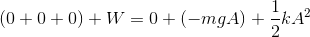
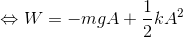
ここで、力のつり合いの式からばね定数kが求められるので、
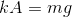
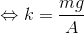
これを力学的エネルギーと仕事の関係式へ代入する。
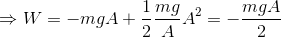
運動量保存則との関係
力学で登場する保存則には3種類あって、それぞれ運動量保存則、力学的エネルギー保存則、角運動量保存則という。このうち角運動量保存則は高校の範囲外なので、次は運動量保存則と力学的エネルギー保存則との関連を調べてみよう。
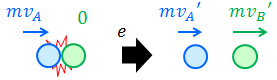
質量mの小球AがvAの速さで、静止している質量mの小球Bに衝突した。その後、A, Bの速さがそれぞれvA', vB'になったとすると、運動量保存則の式は、
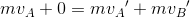
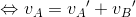
であり、また、このときの反発係数をeとすると、反発係数の式は
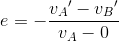
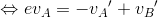
になる。これらを解くことで、衝突後のA, Bの速さをそれぞれ求めることができる。
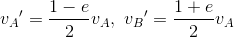
それでは続いて力学的エネルギーの変化ΔE(=今は運動エネルギーの変化)を求めよう。衝突前の力学的エネルギーEは、
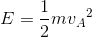
であり、衝突後の力学的エネルギーE'は
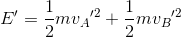
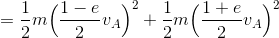
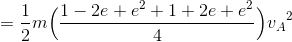
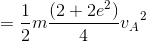
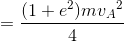
である。よって、ΔE=E'-Eは
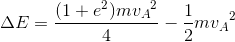
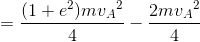
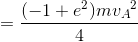
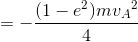
になる。このことから、2物体の衝突のとき
- e=1のとき、力学的エネルギーが保存(ΔE=0)
- e<0のとき、力学的エネルギーが減少(ΔE<0)
ということが分かる。つまり、弾性衝突の場合にのみ、力学的エネルギーが保存されるのだ。非弾性衝突の場合(e<0)には、衝突前の力学的エネルギーが物体の変形という仕事に使われてしまい、衝突後も元の形には戻らないのである。
